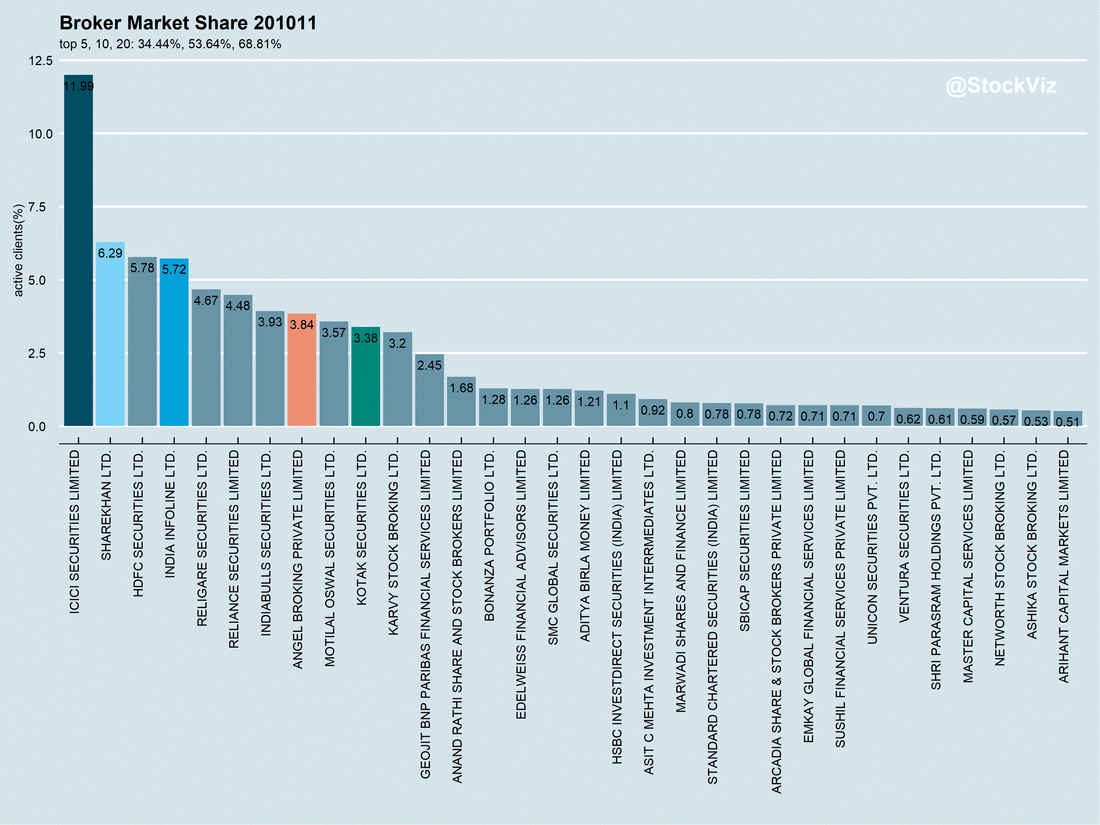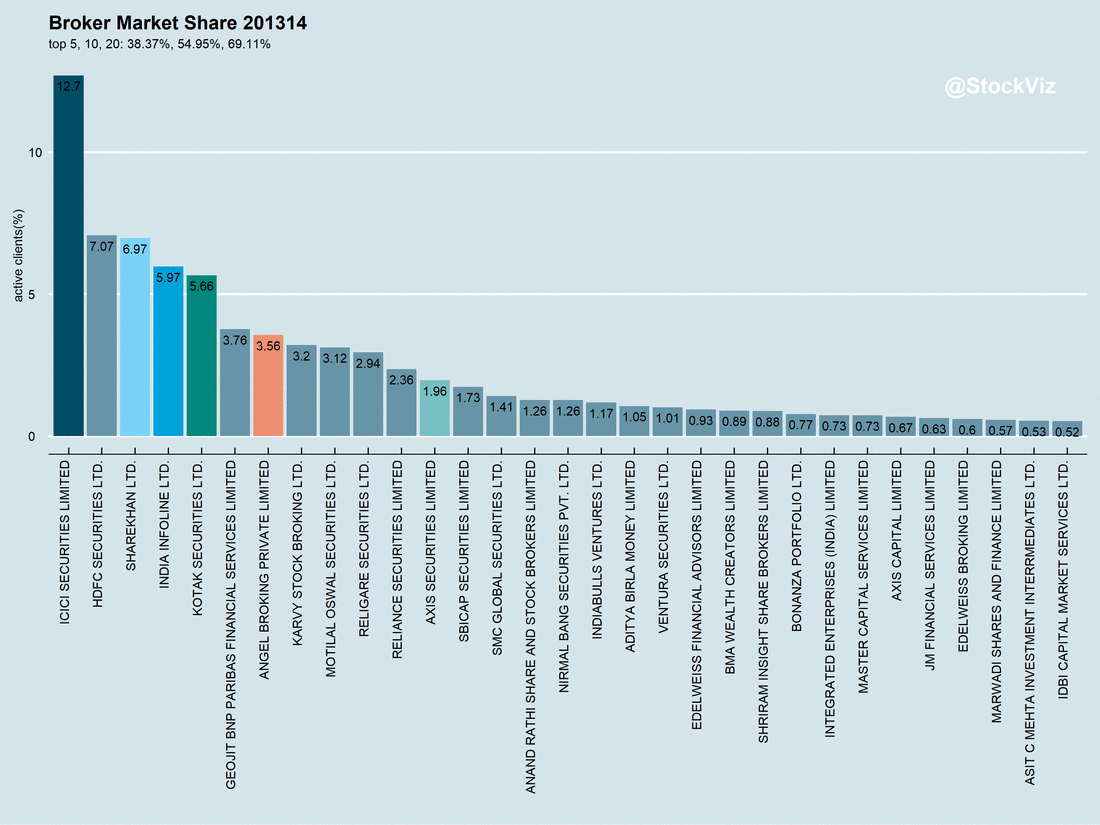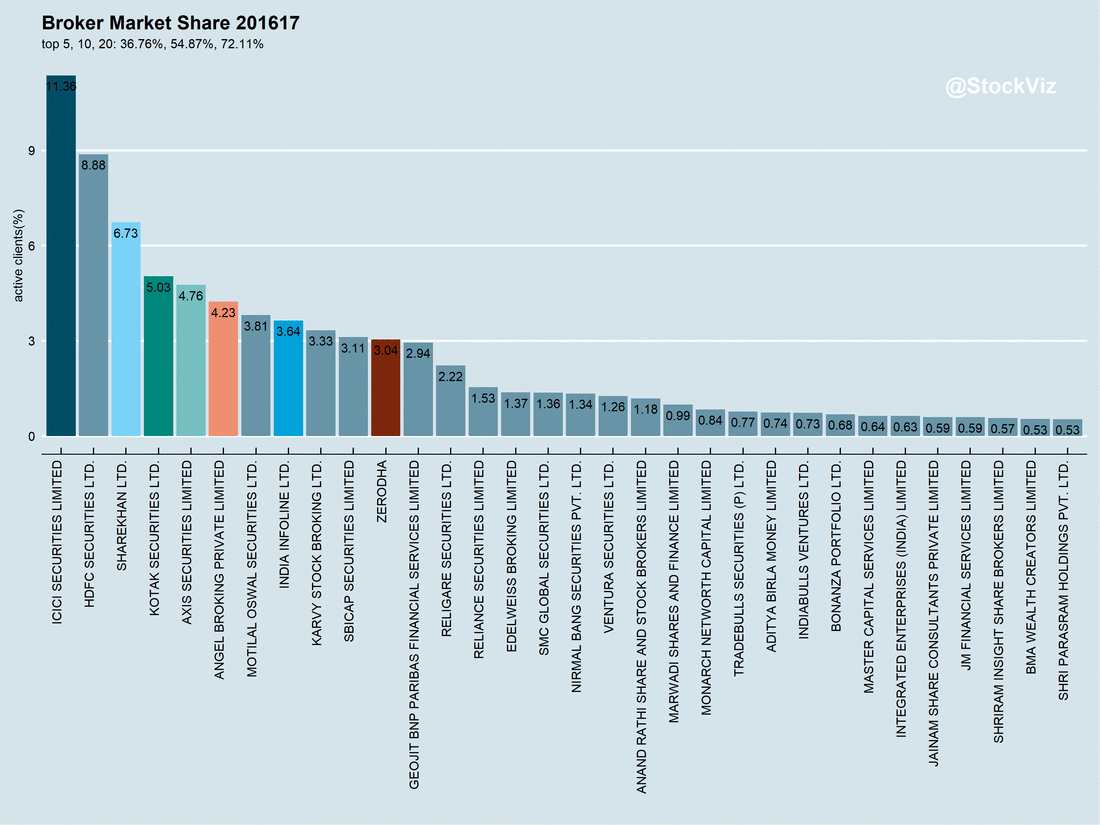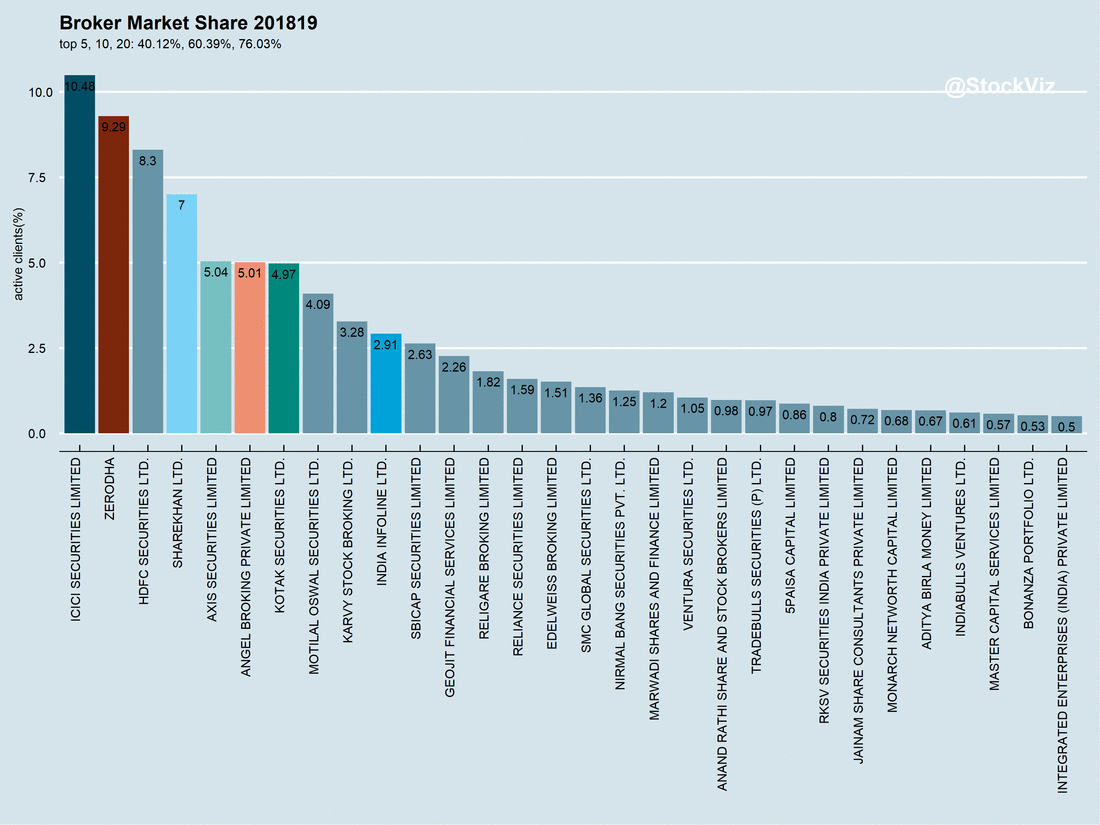
The following post is a replication of the Newfound Research article When Simplicity Met Fragility (pdf)
Thesis
Returns are function of both luck and skill. Even while applying systematic strategies like trend-following, momentum or value, there is always negative beta that sometimes overwhelms positive alpha. The article shows that “simple” strategies are often “fragile” because of the role of randomness (luck.) So it makes sense to combine different strategies within the same umbrella to make the investment process more robust. For example, there are more than a few dozen ways to implement a momentum strategy. Combining a few of them will result in a portfolio that is less exposed to luck.
Replication results
We used R to replicate the process described in the article on the S&P 500 index. We downloaded index values from Yahoo Finance and put through the same steps. Here is the single-strategy spread chart that uses 12-1 month momentum:

And this is the multi-strategy spread chart that combines three trend-following strategies including the one above:

As you can see, the multi-strategy chart is a lot less choppy that the single-strategy one. We will chalk this up as a successful replication of the original article.
The NIFTY 50 experience
Would the thesis hold when applied to the NIFTY 50 index?
Here is the single-strategy spread:

And here is the multi-strategy spread:

As you can see, the multi-strategy chart is a lot less choppy that the single-strategy one on the NIFTY 50 index as well.
Take-away
By combining different approaches under the same systematic strategy umbrella, investors can reduce the fragility of their overall portfolio and the influence of luck over the investment outcome.
This is something that we have been doing with our Themes right from the beginning. It just felt like common-sense back then. It is nice to see it in numbers.
Code and charts are on github.