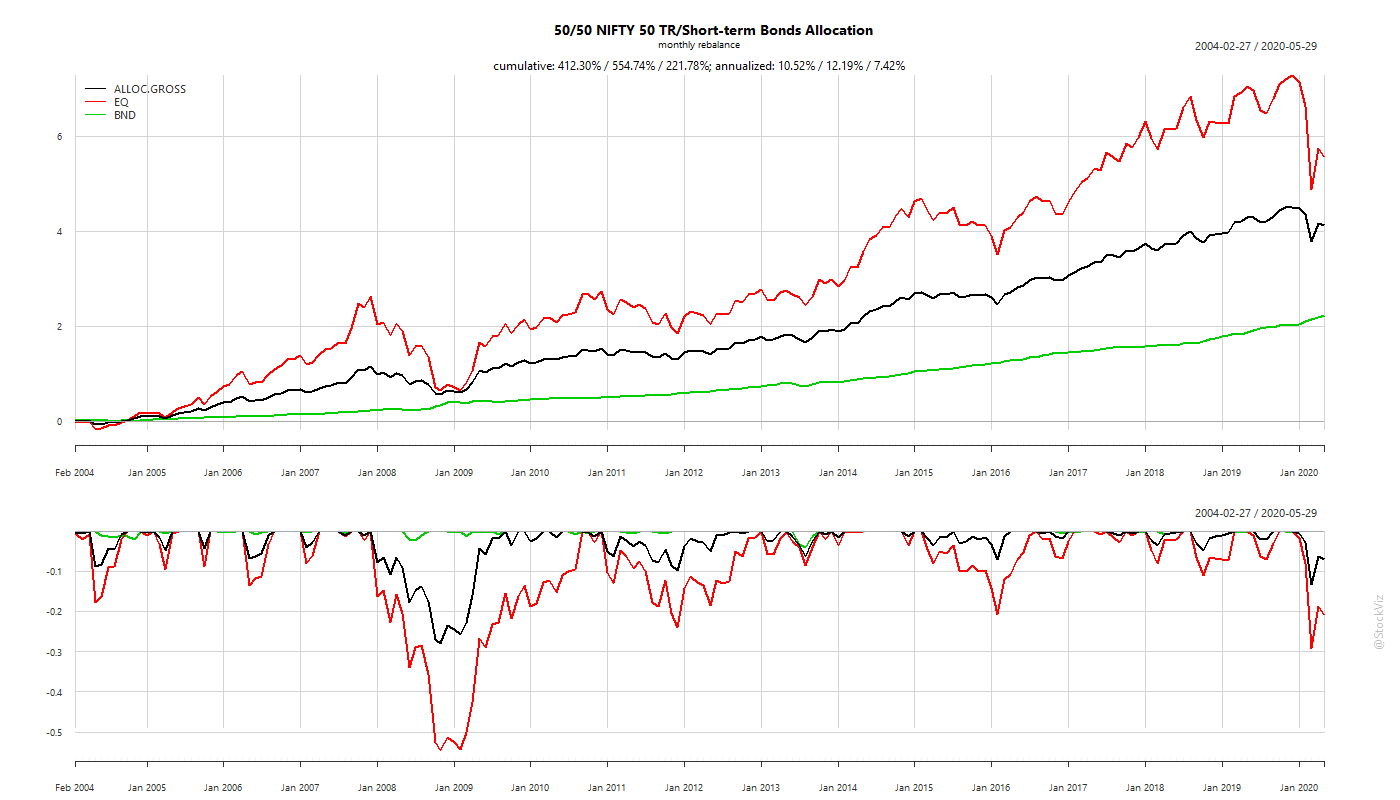
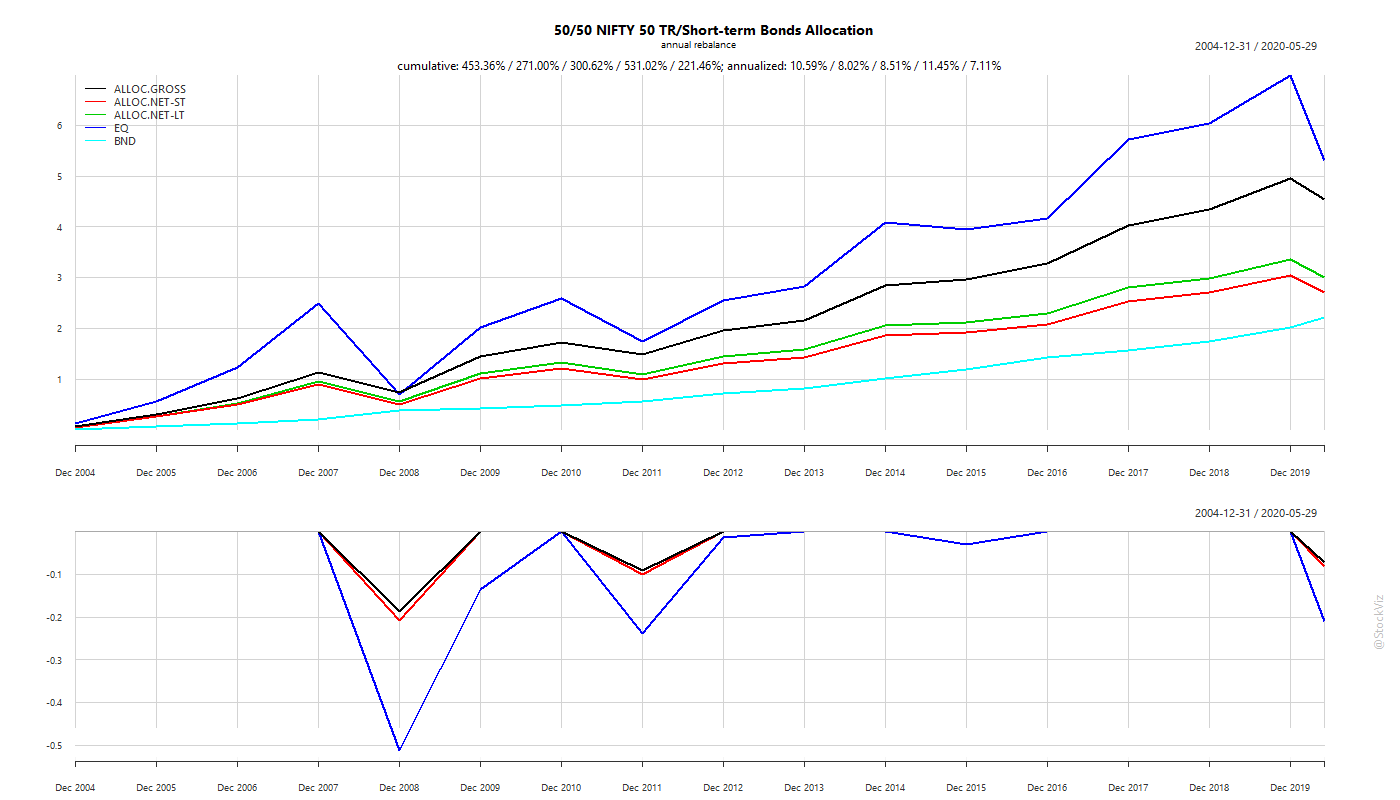
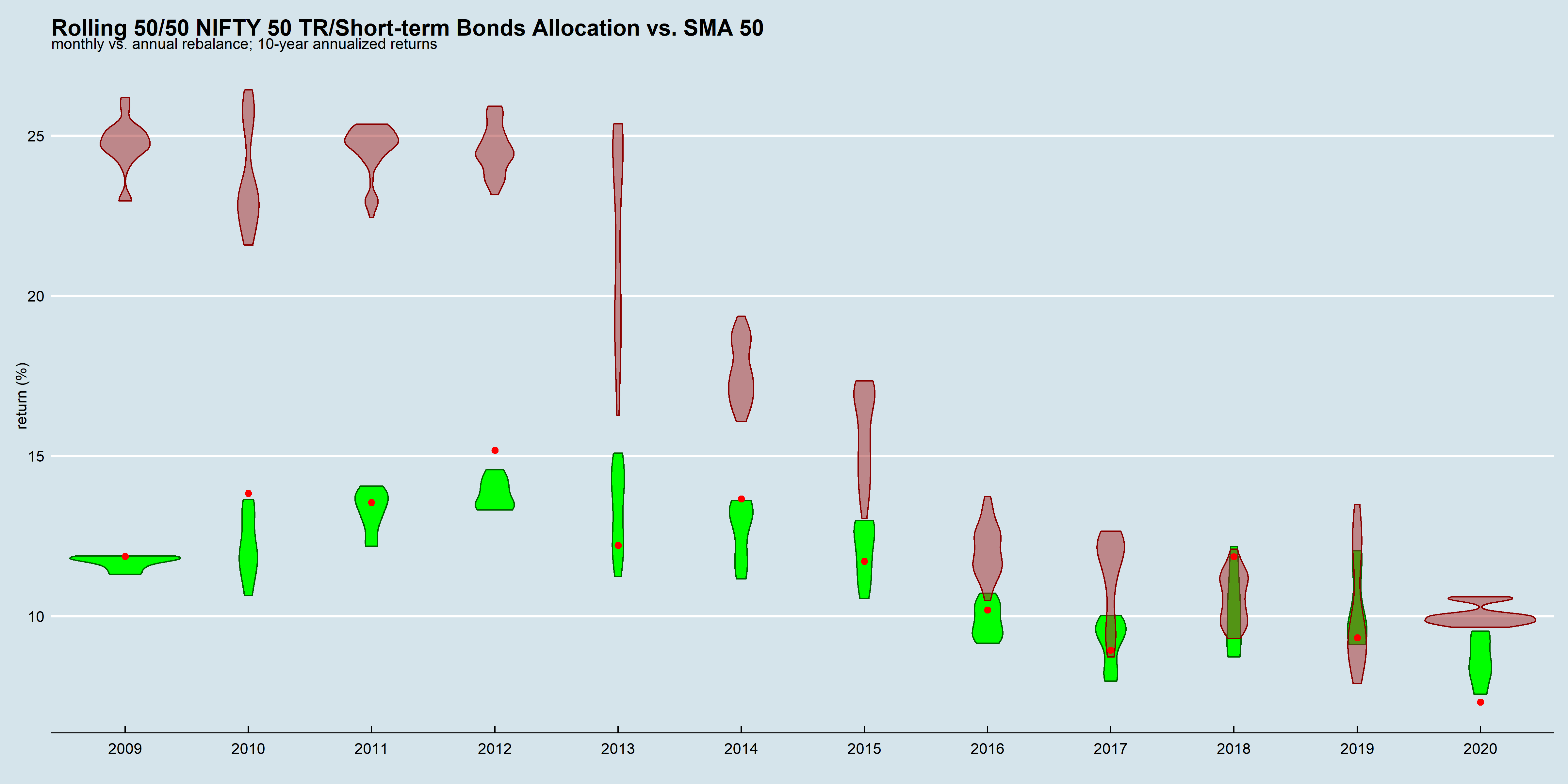
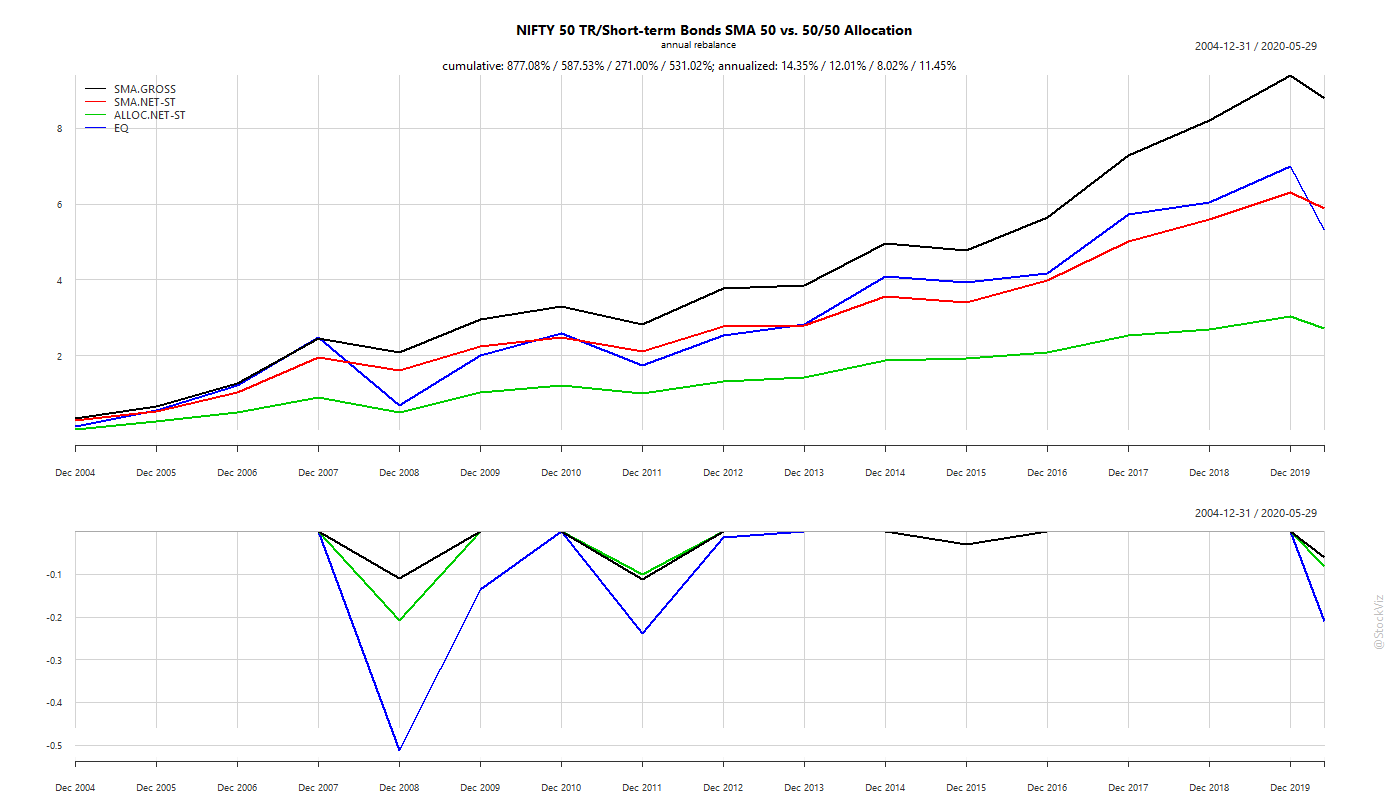
Think in terms of volatility buckets, not assets
This post is part of our series on diversification and asset allocation. Previously:
The thrust of our previous posts on allocation was that Indian investors shouldn’t blindly copy strategies that worked well in the US. There are a lot of qualitative arguments to be made to support a India-dominant view for allocation strategies. In this post, we introduce a quantitative aspect to the discussion.
It is Volatility, Stupid!
In finance, more than any other field, it is very easy to get correlation and causation mixed up.
A man goes to the doctor and says, “Doctor, wherever I touch, it hurts.”
The doctor asks, “What do you mean?”
The man says, “When I touch my shoulder, it really hurts. When I touch my knee – OUCH! When I touch my forehead, it really, really hurts.”
The doctor says, “I know what’s wrong with you. You’ve broken your finger!”
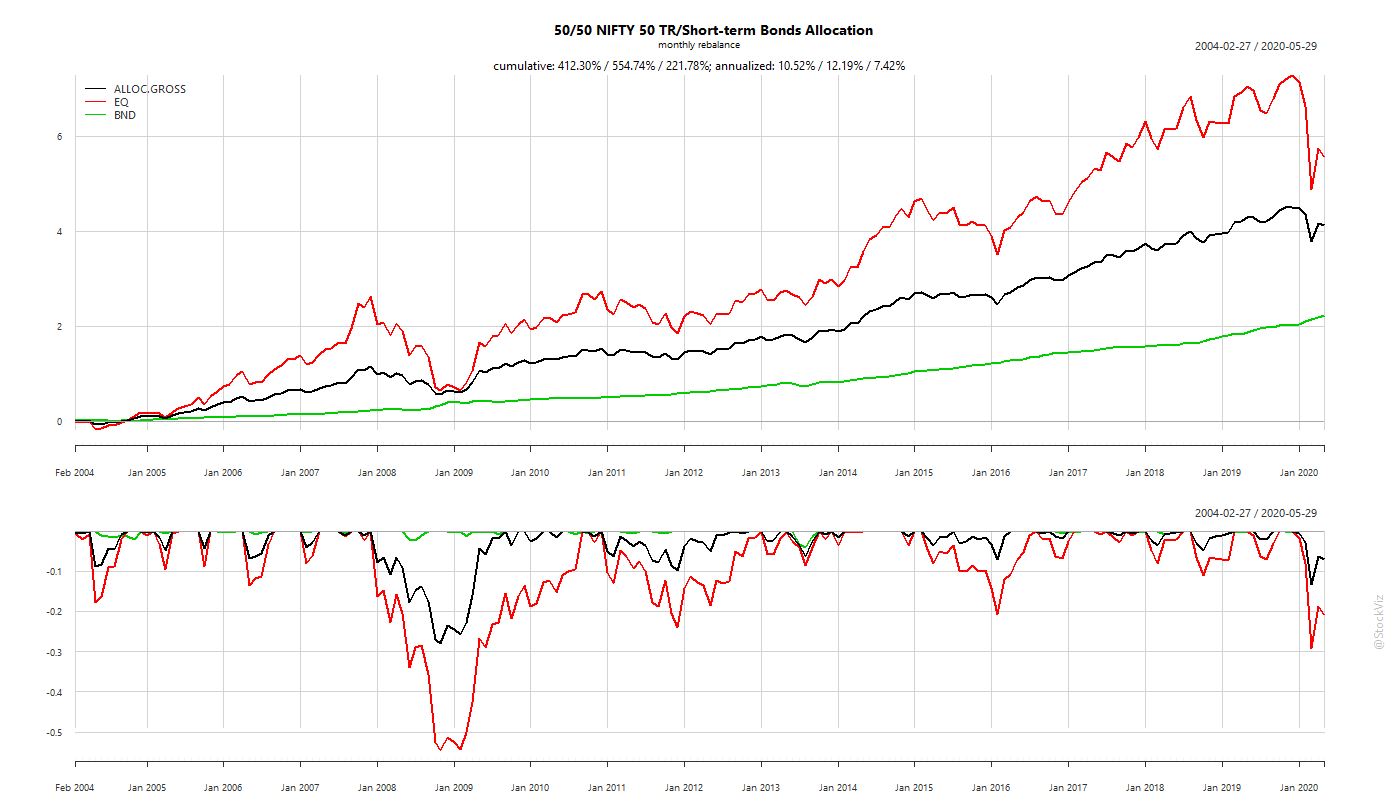
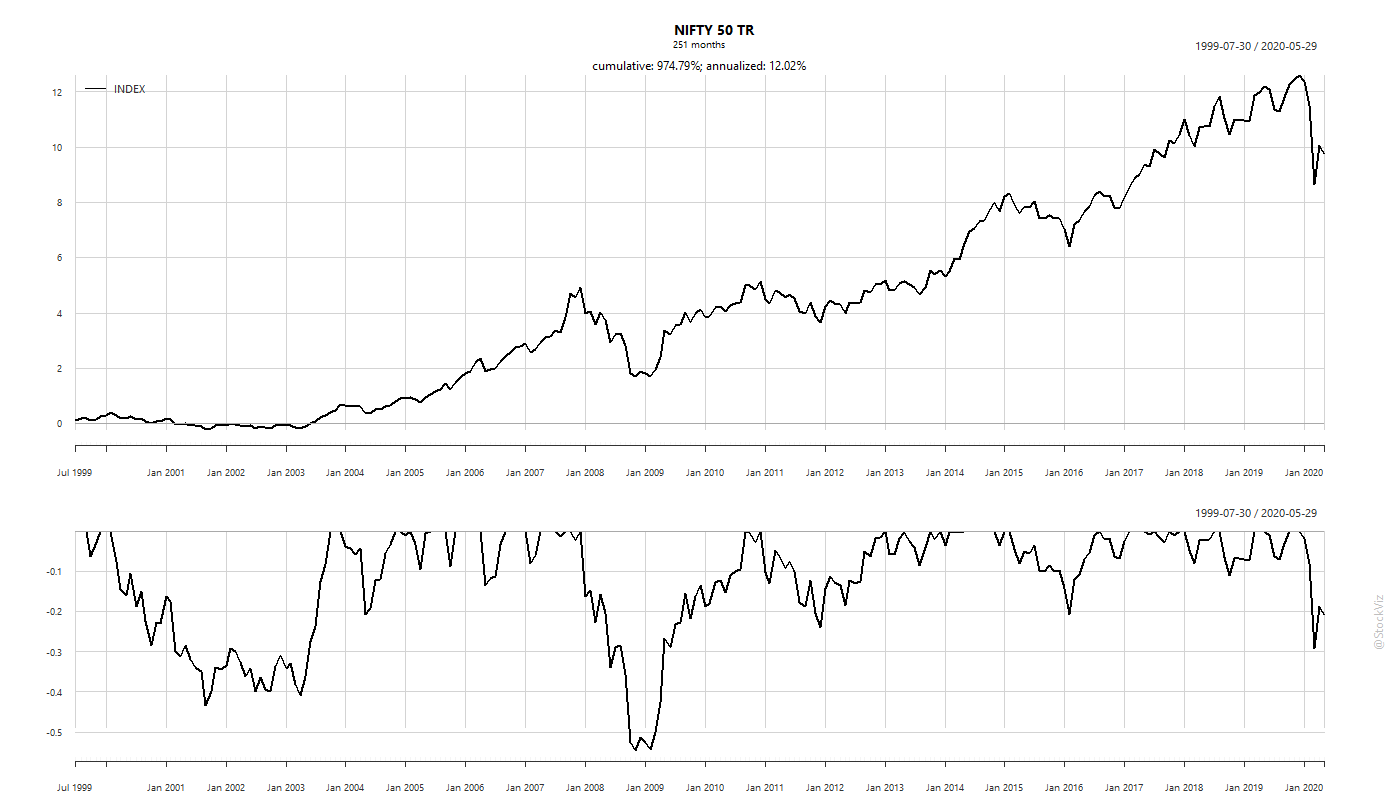
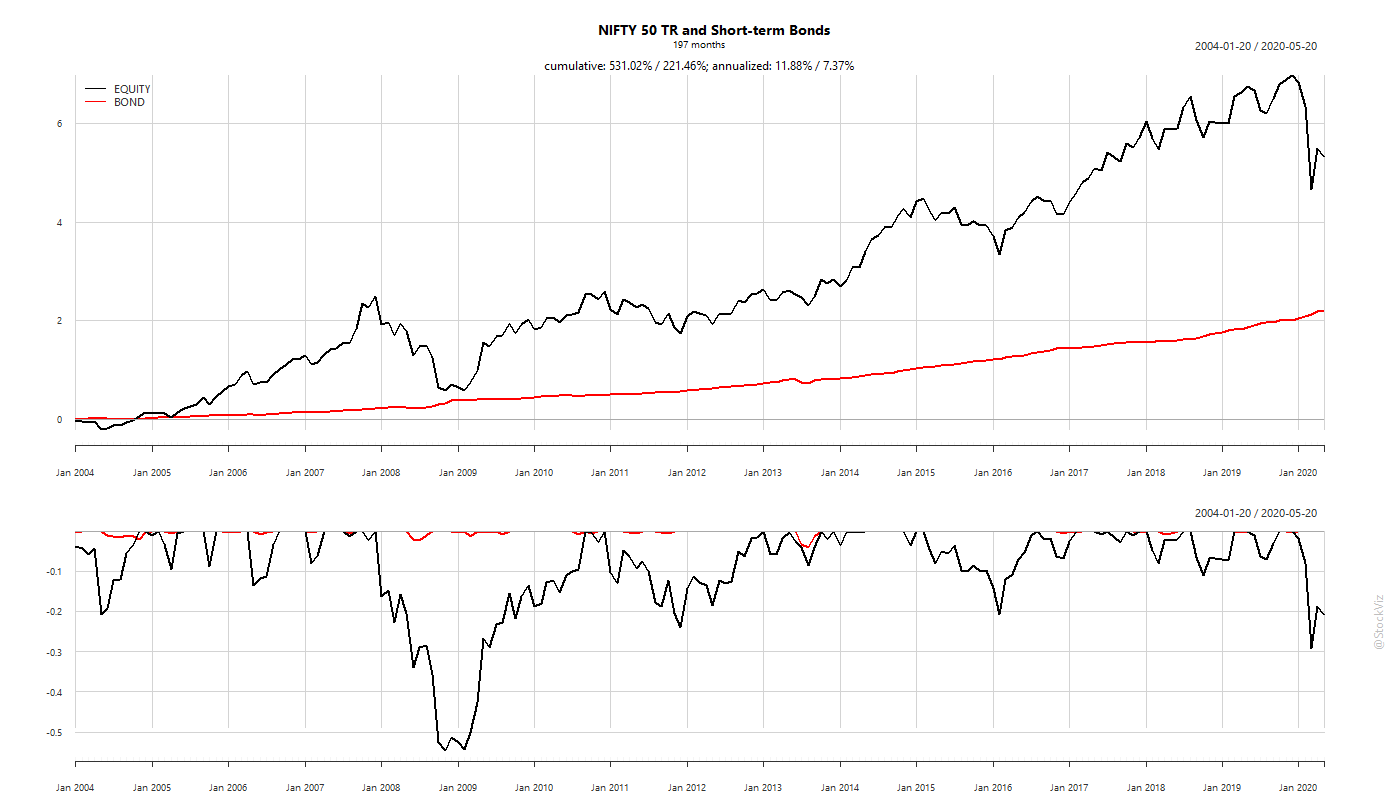
There are no universal laws for an asset class that holds across geographies and economic systems. The reason why a 60/40 Portfolio “works” in the US has more to with the quantitative aspects of the assets being mixed than what they are called. US bonds have benefitted greatly from a 30 year slide in yields, benign inflation and a flight-to-safety bid. None of these hold true for Indian bonds. So, expecting a 60/40 Indian portfolio to behave like a 60/40 US portfolio just because you mixed the same assets together is idiotic.
The most import aspect while considering assets for diversification are their volatilities. Specifically, the correlation of their volatilities at their left tails.
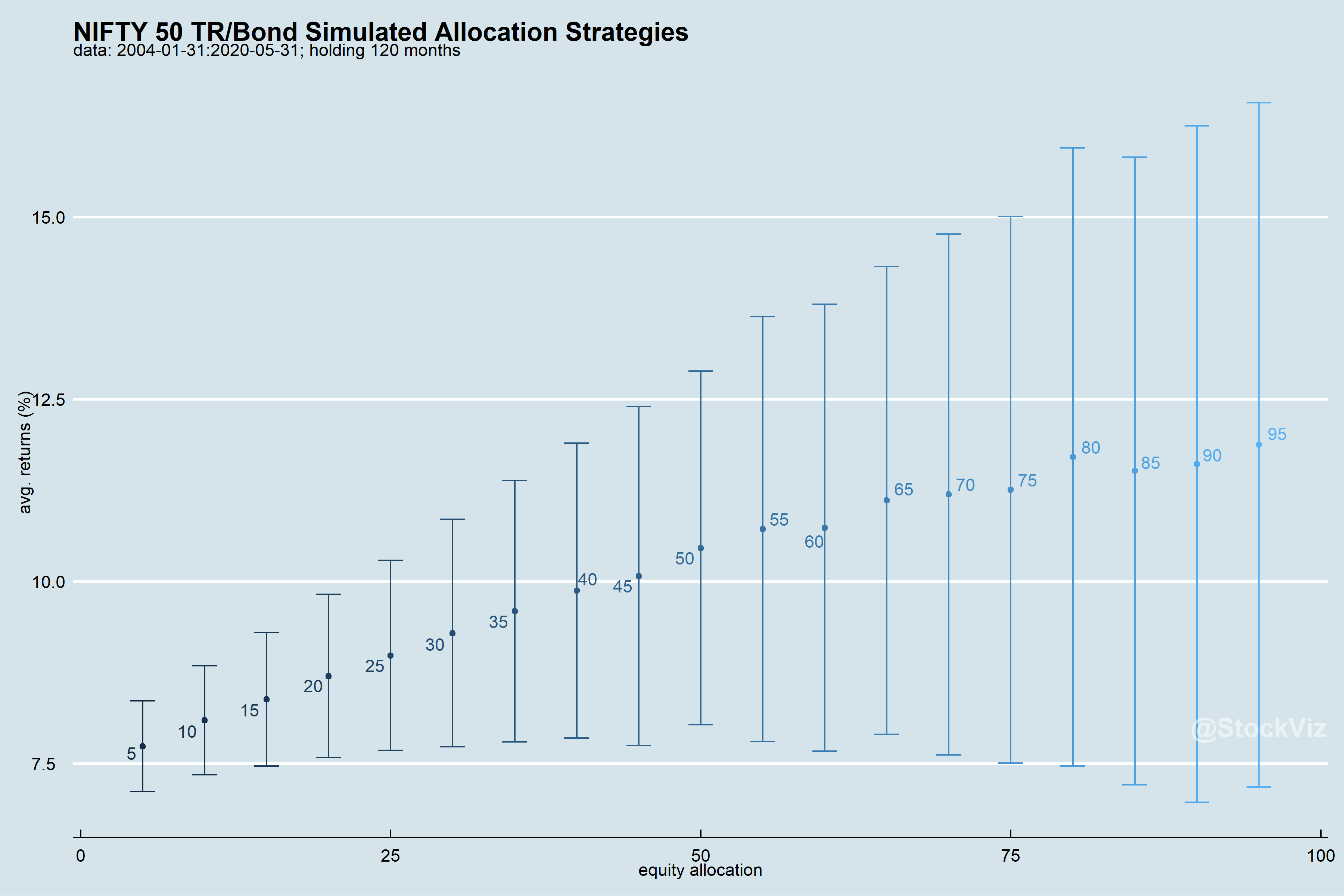
To keep things simple, consider a 2 asset portfolio: Eq and X. Eq has some average return that will be held constant during this analysis. What changes is its standard deviation (aka, volatility.) X is a stable asset with zero volatility (think of it as a fixed deposit.) How does different allocations to Eq change portfolio returns and volatility?

Low volatility is supportive of higher allocations
Higher allocations to the higher volatility asset progressively reduces the predictability of portfolio returns
Volatility is Volatile
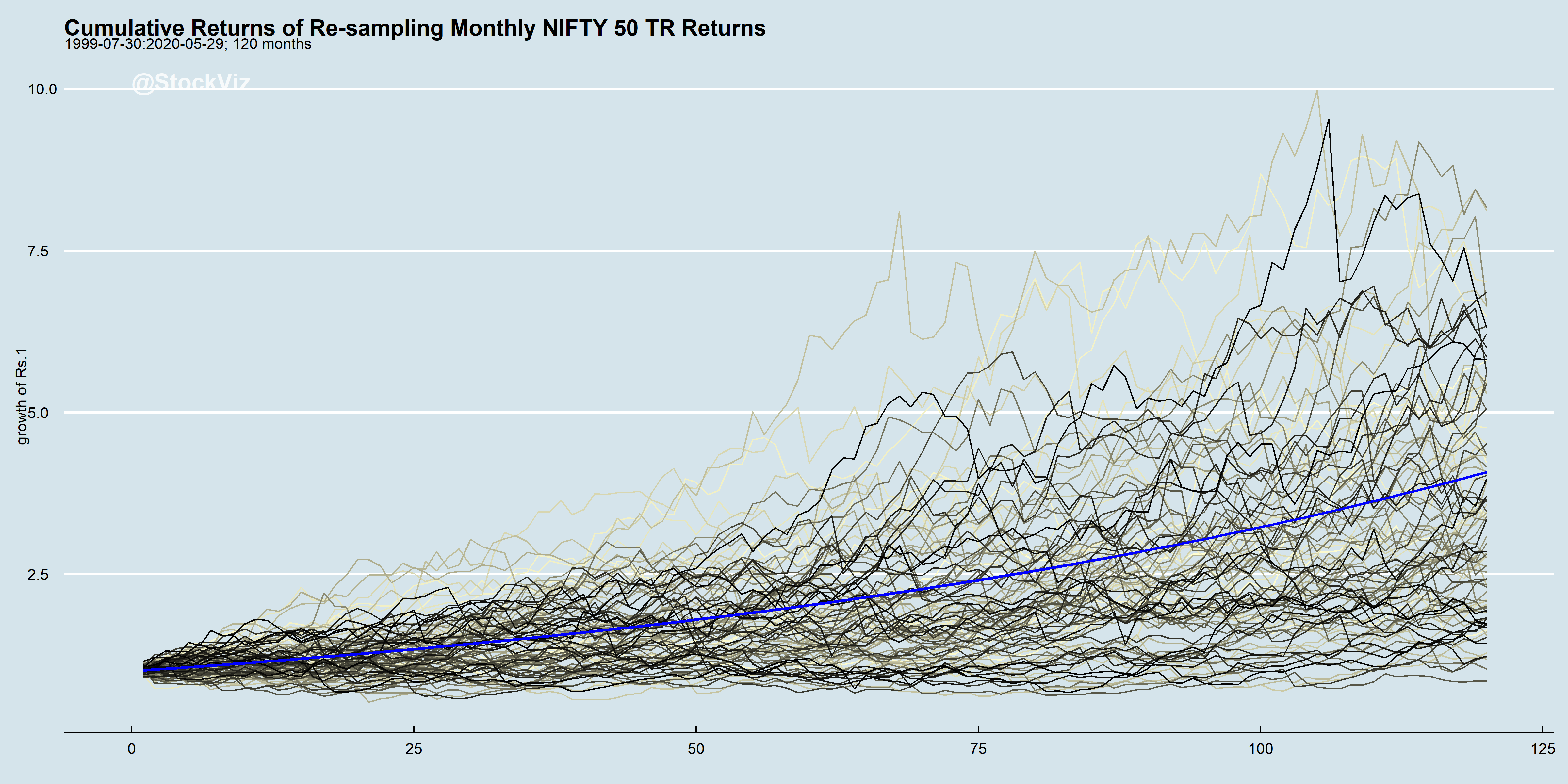
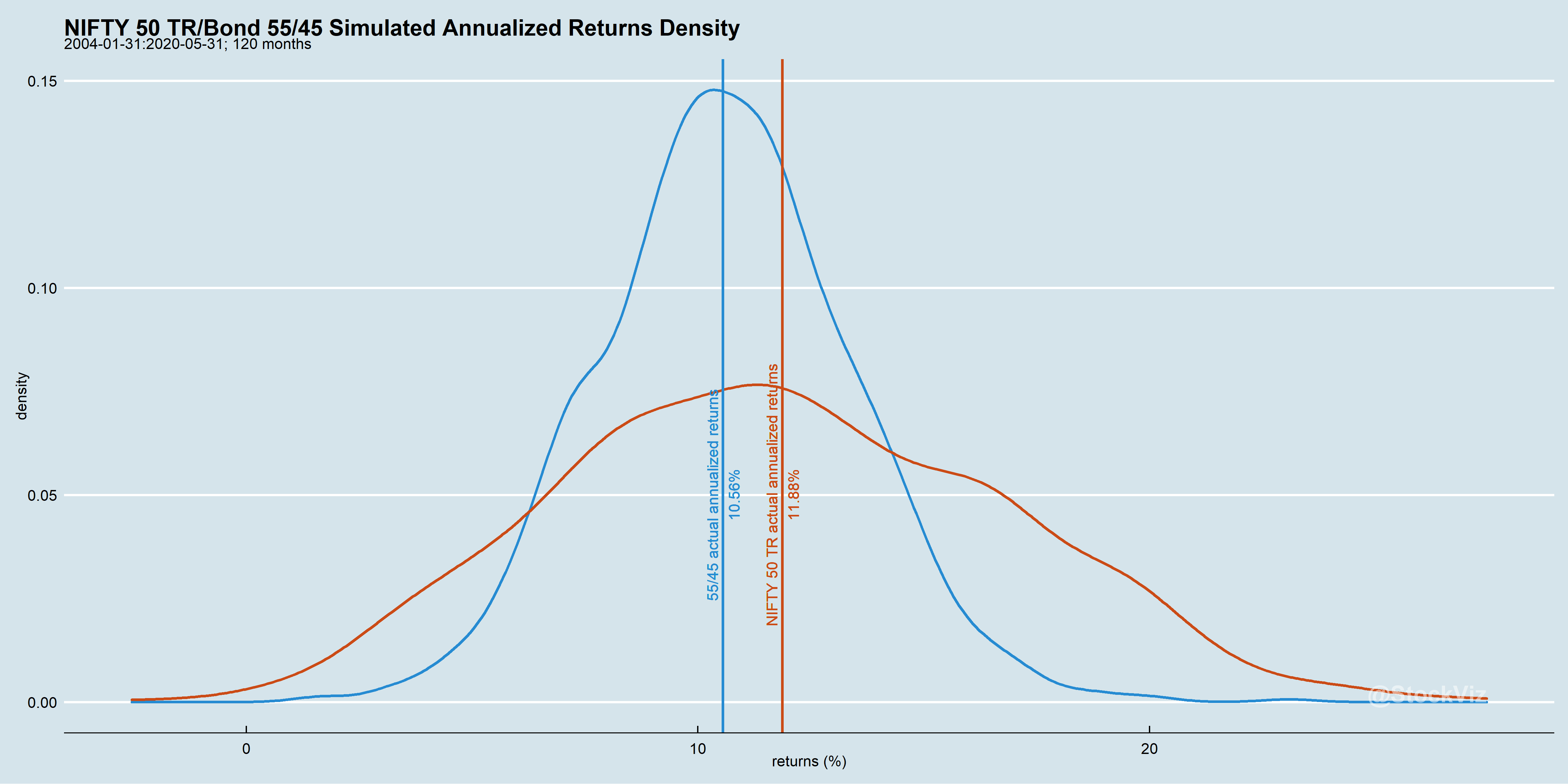
Asset return volatility is itself volatile.

The past performance of a diversified portfolio is based on the realized volatility of its components. However, volatility itself is unpredictable over long periods of time.
Take-away
While considering assets to diversify into, look at the volatility of the asset rather than what it is called.
Don’t expect the quantitative aspect of an asset class to transcend economic systems – different markets need different treatments.
All investing is forecasting. And all allocation is forecasting volatilities.