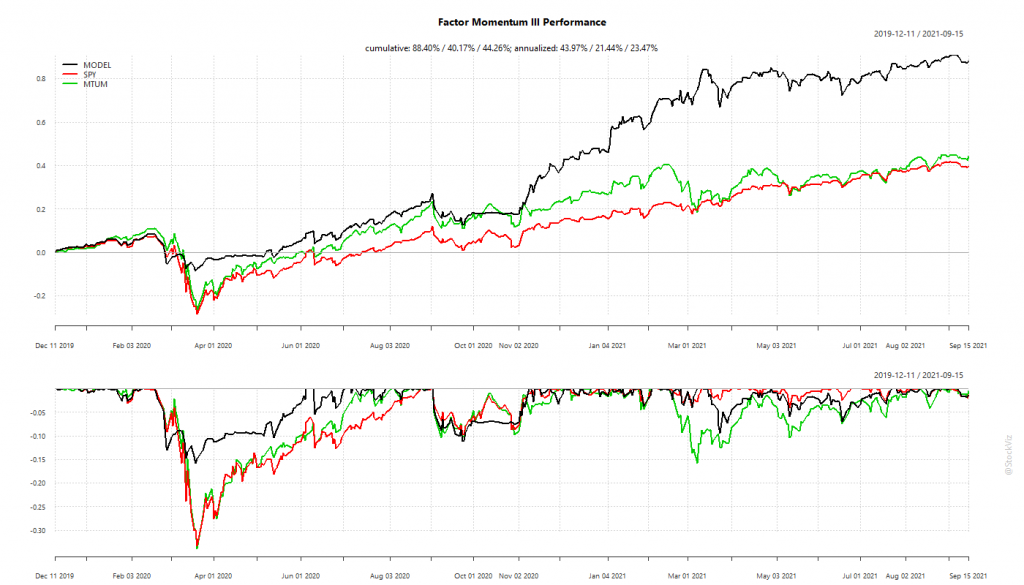
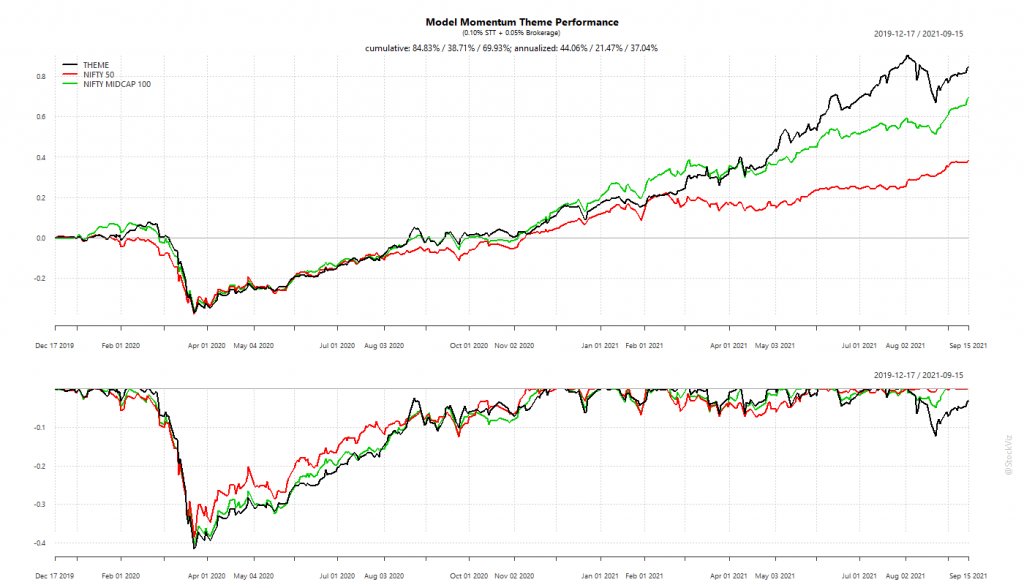
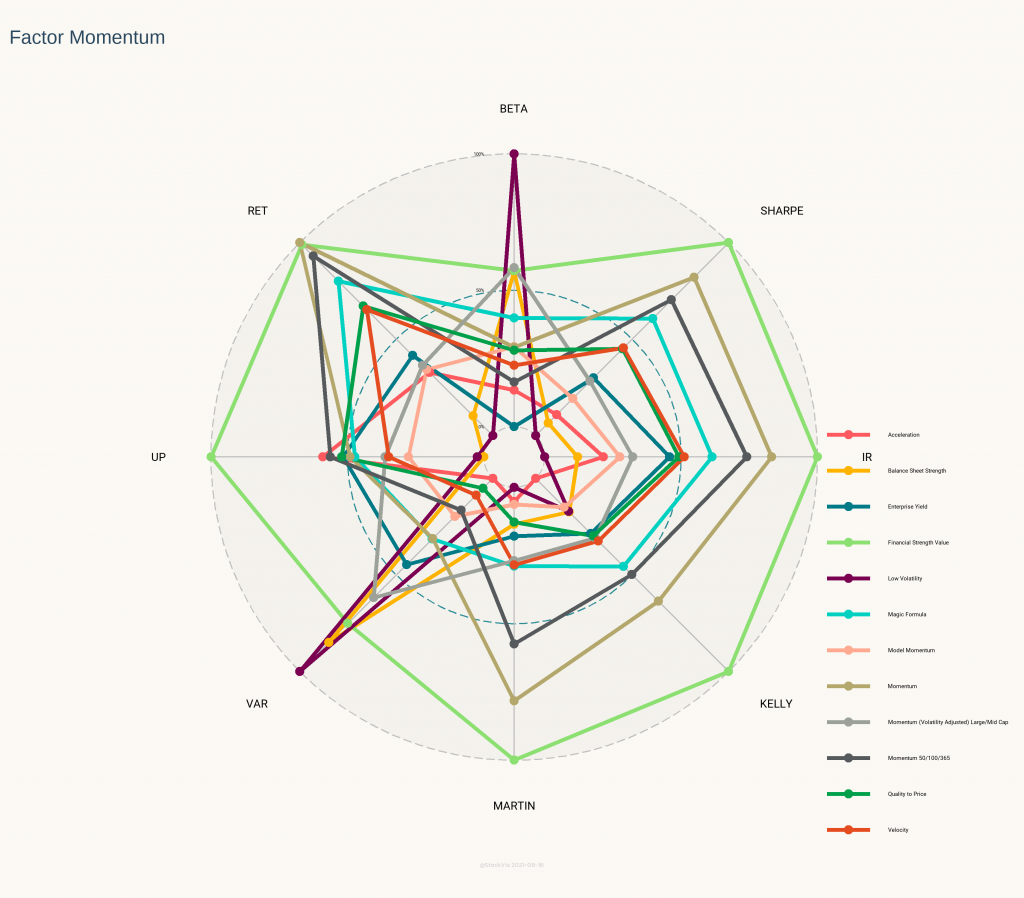
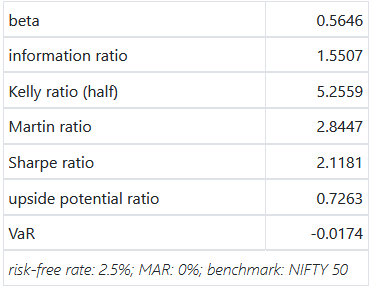
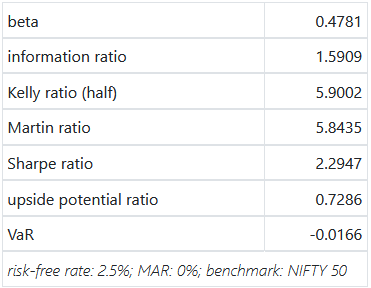
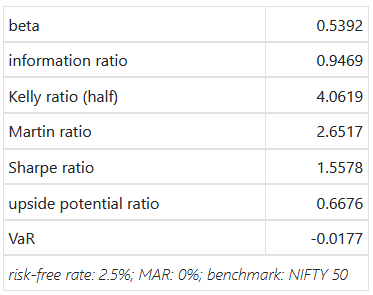
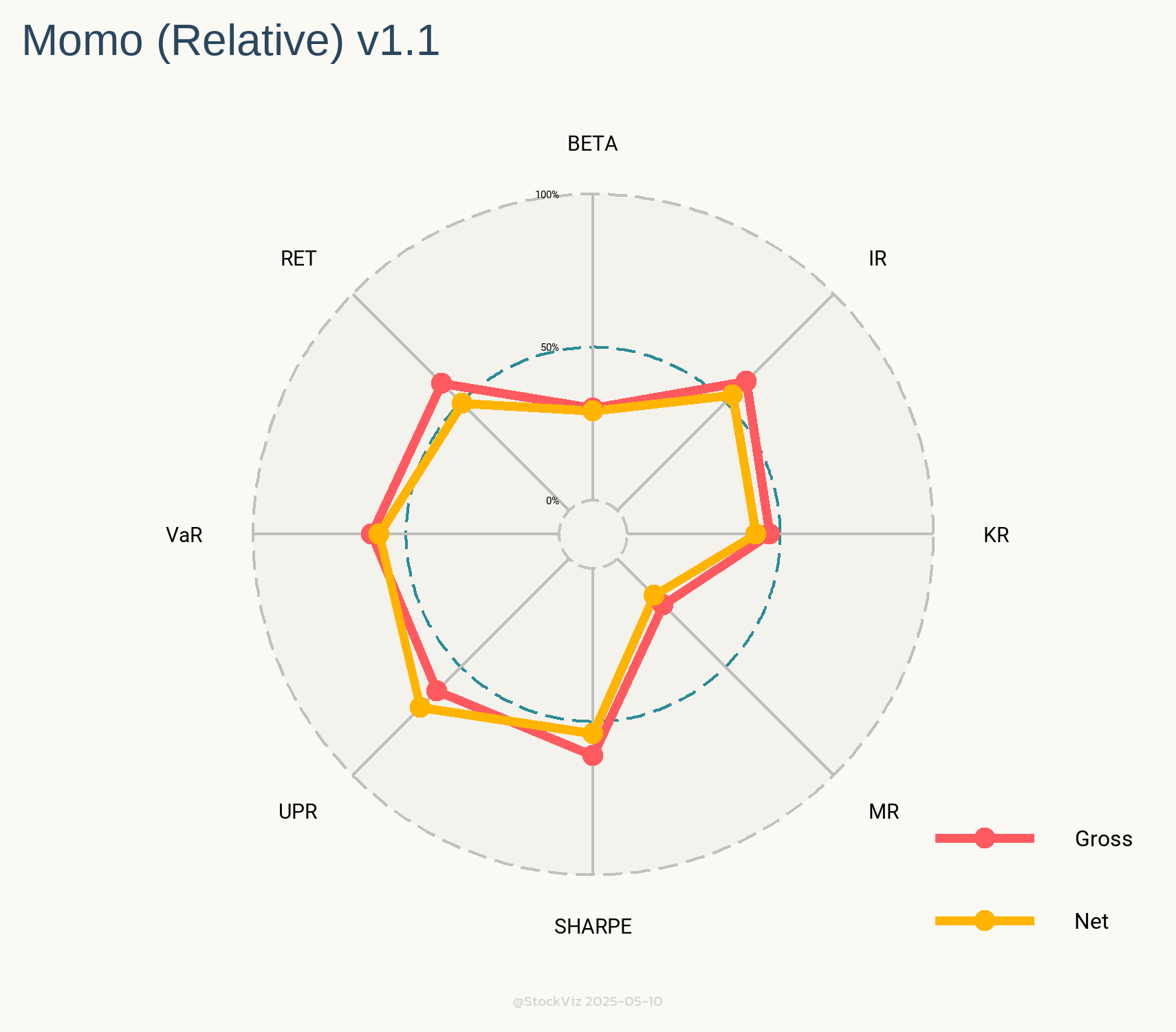
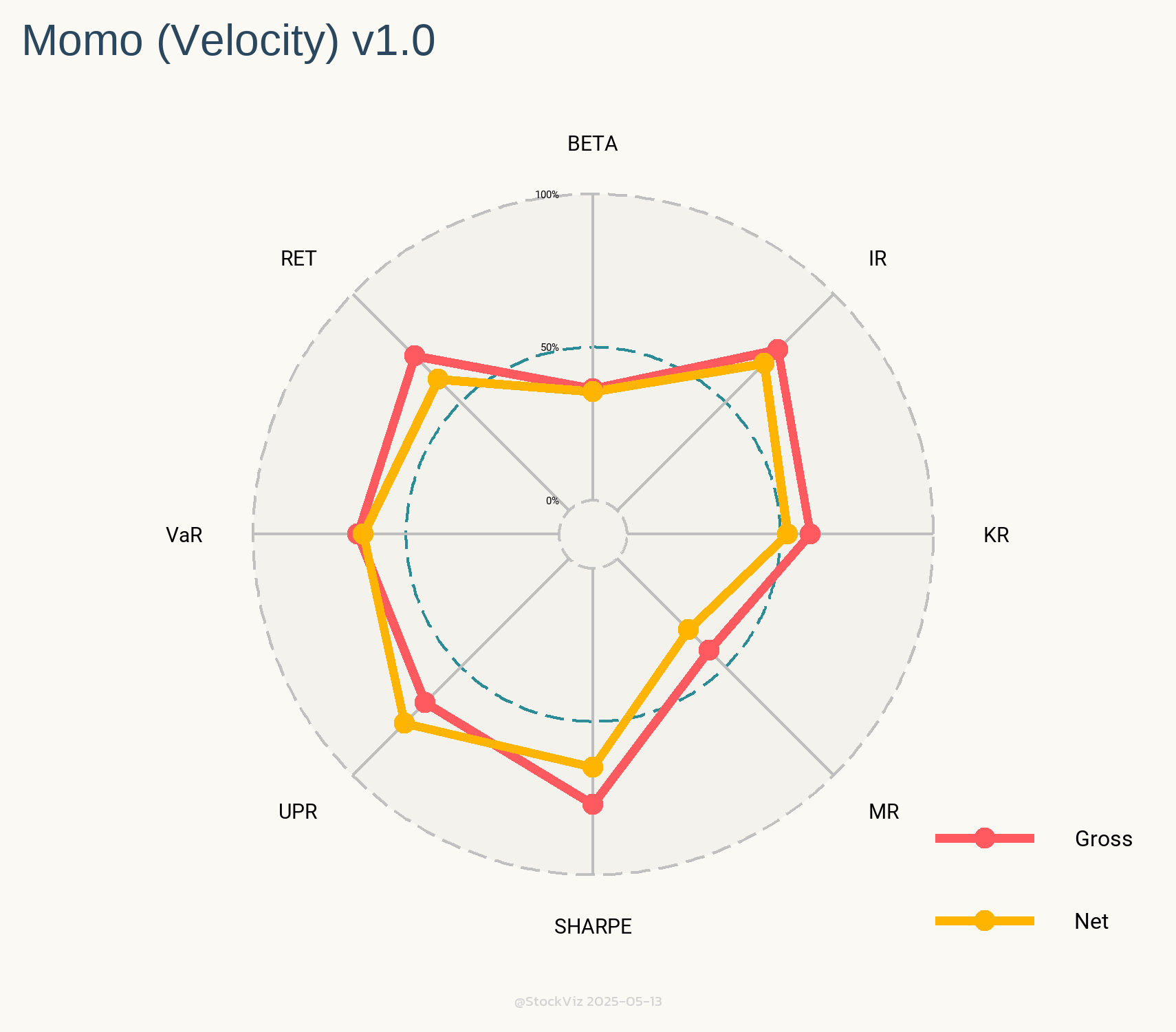
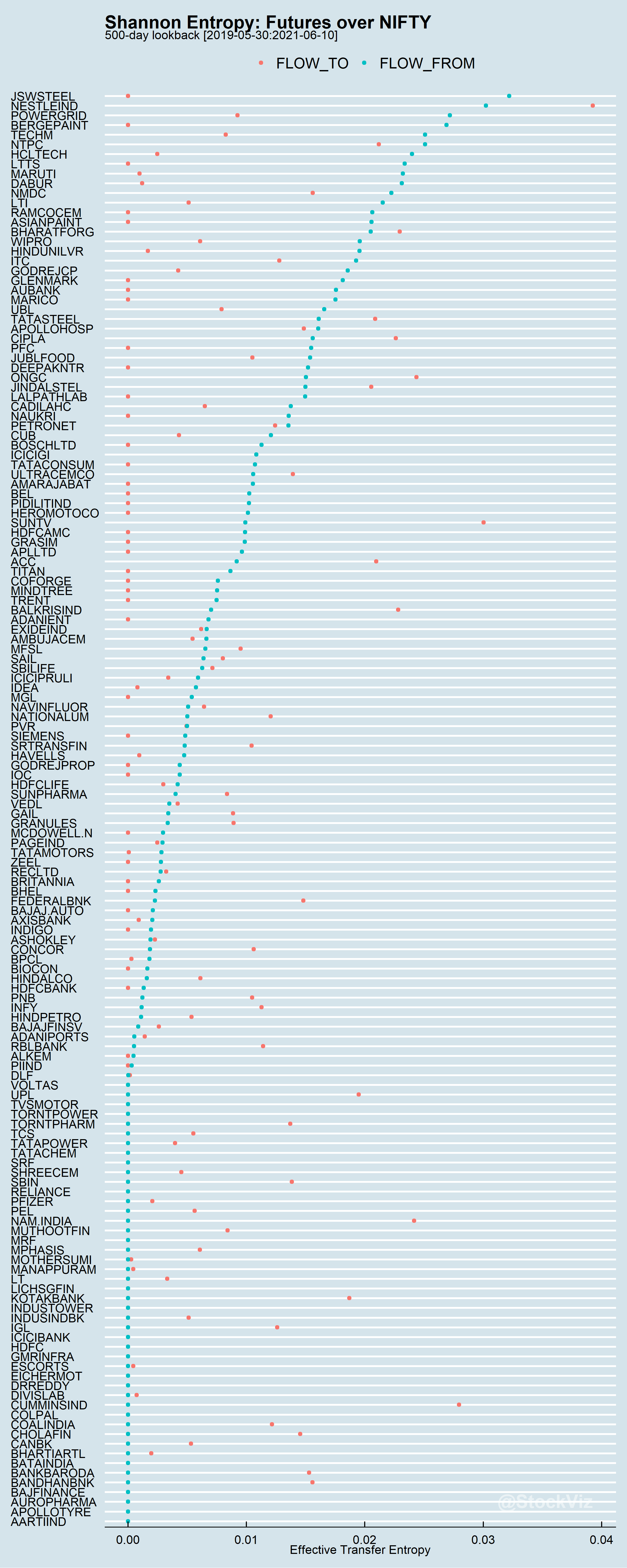
While introducing S&P 500 sector ETFs, we showed how the cross-correlations between them were unstable. This makes developing simple strategies challenging. One common momentum strategy is to simply go long whatever worked best in the previous period.
Rules of Rotation
For ETFs: XLY, XLP, XLE, XLF, XLV, XLI, XLB, XLK, XLU, and SPY
- Calculate rolling returns over n months. Where n = 1, 3, 6, 12.
- For the n+1th month, go long the ETF that had the highest return in Step 1.
- In Step 2, if the selected ETF has -ve returns, stay in cash and earn zero.
We split the dataset into Before 2010 and After 2011.
Pick your Fighter
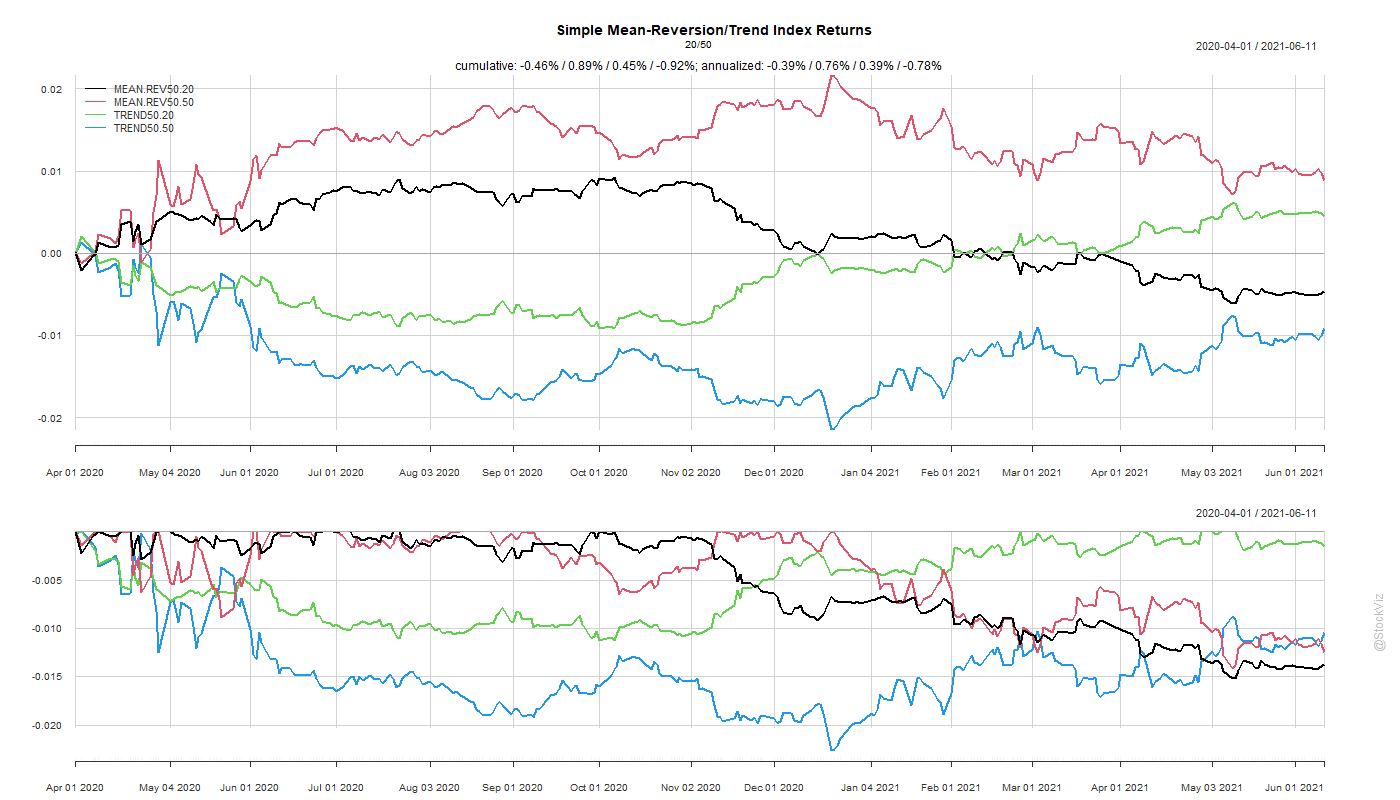
The Before 2010 dataset shows rotation by all look-back periods to be better than buying-and-holding the S&P 500.
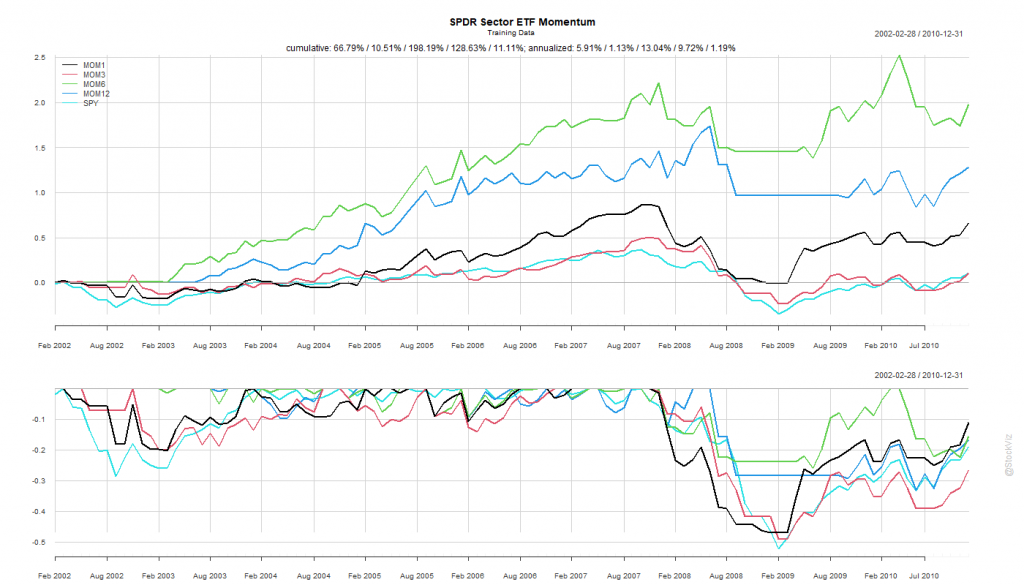
Probably because of the prolonged dislocation caused by the GFC in 2008 and 2009, all rotation strategies based on the rules above exhibited great stats.

The SPY Rope-a-Dope
In boxing parlance, a “Rope-a-Dope” is
When you maintain a defensive posture on the ropes in an attempt to outlast or tire your opponent. It is most recognized and was actually given that name by Muhammad Ali when he employed the technique to defeat George Foreman.
titleboxing.com
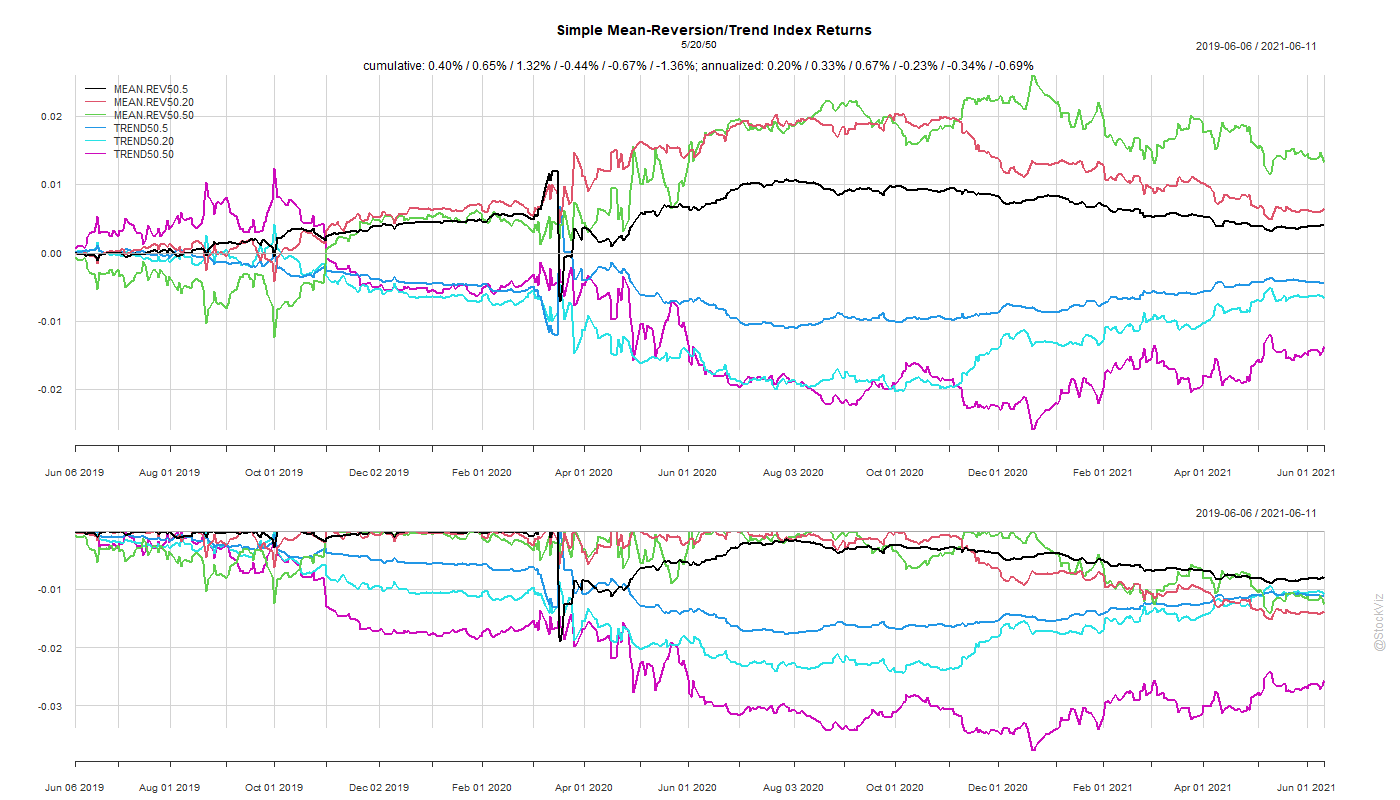
The After 2011 dataset is a prime exhibit of why “sure-things” don’t exist in finance.
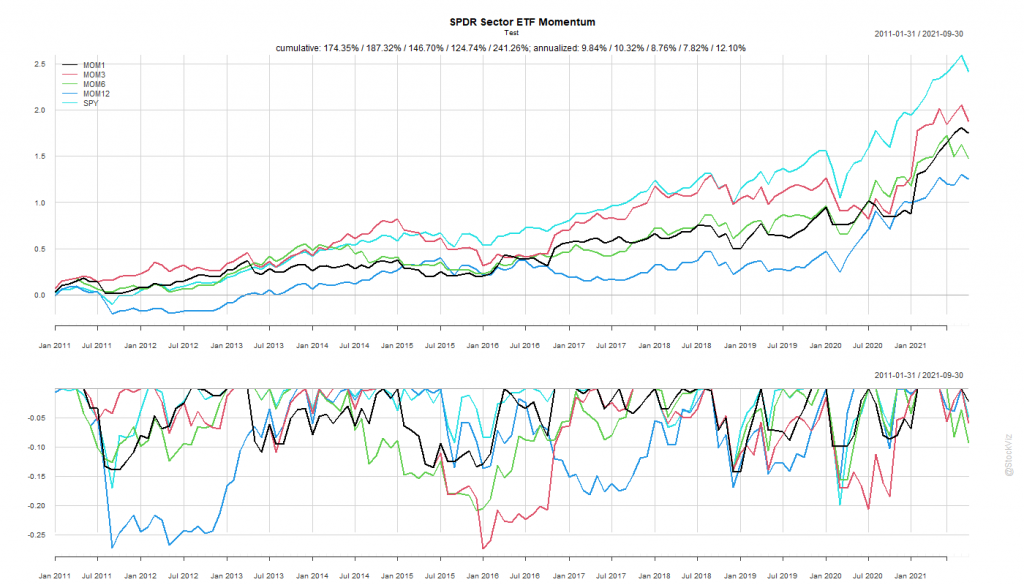
The S&P 500 spent the next decade demolishing everything.

MOM6, the winner from our first round, went on to underperform the S&P 500 for the next 10 years by ~4%
By simply holding onto the ropes, a passive buy-and-hold S&P 500 investor would’ve come out miles ahead of someone who employed this rotation strategy.