Our previous posts showed how various allocation decisions impact optimized and equal-weighted three-asset portfolios. Here, we add a fourth asset – gold – and run it through the same scenarios.
Picking the Assets and Allocation
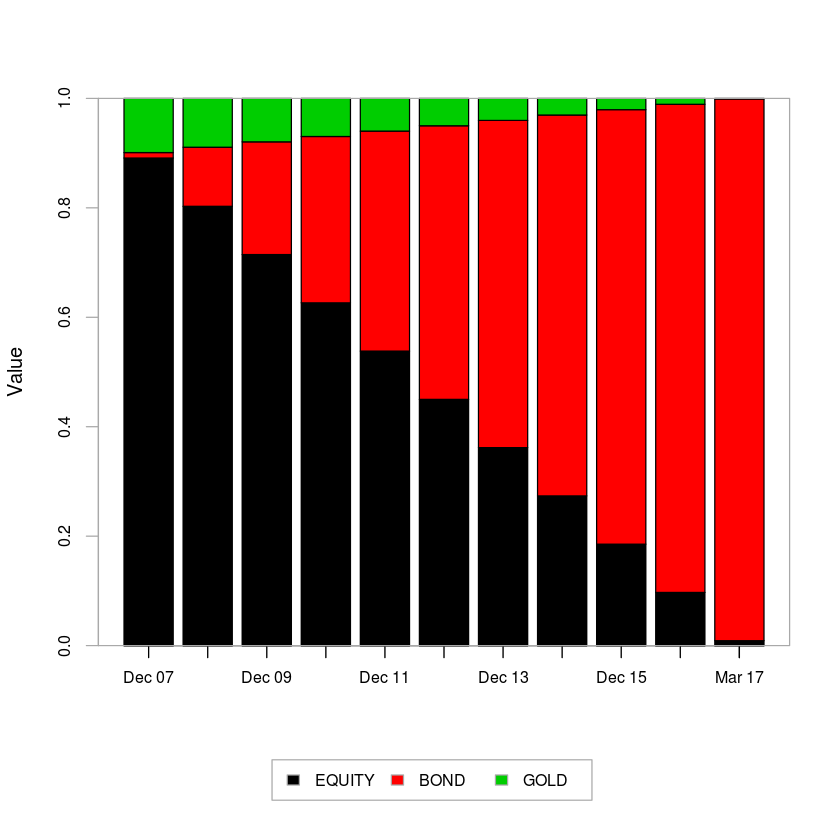
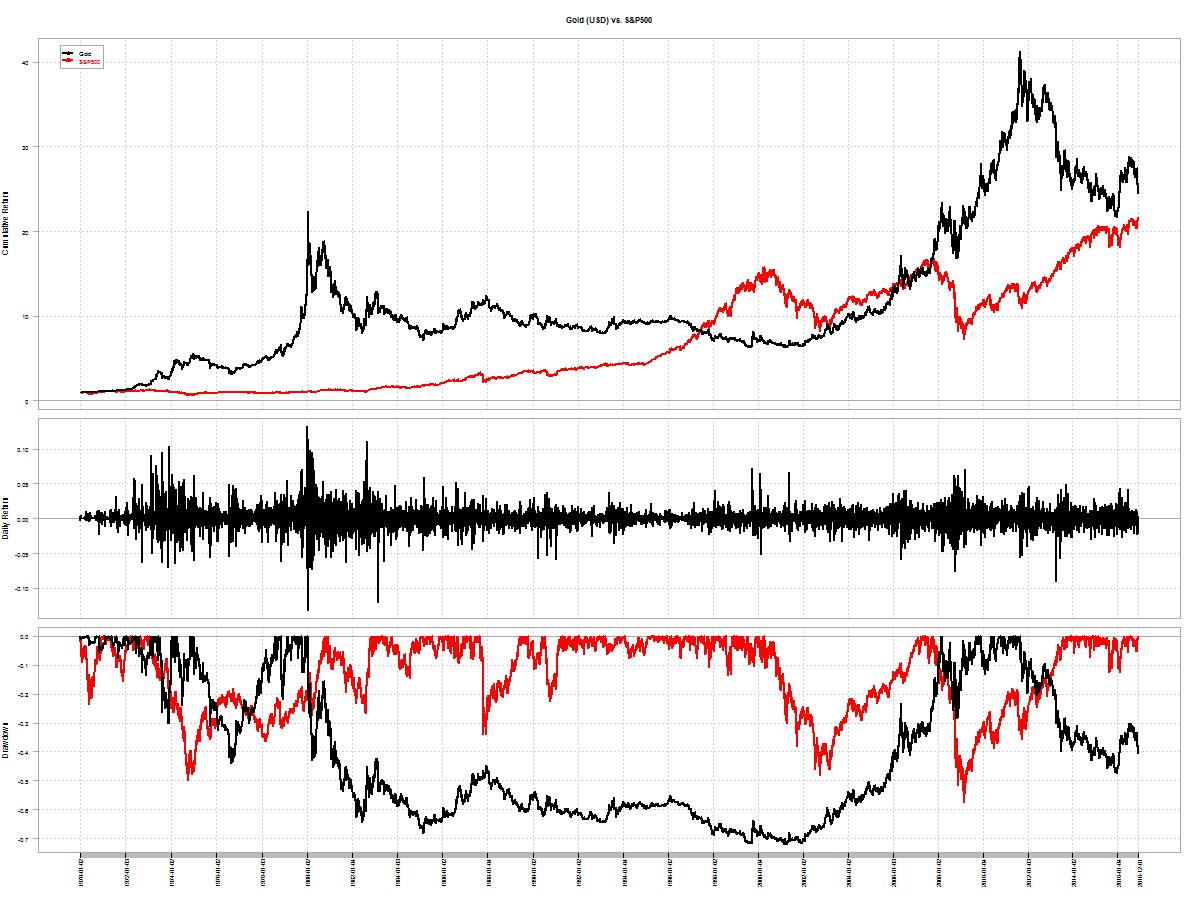
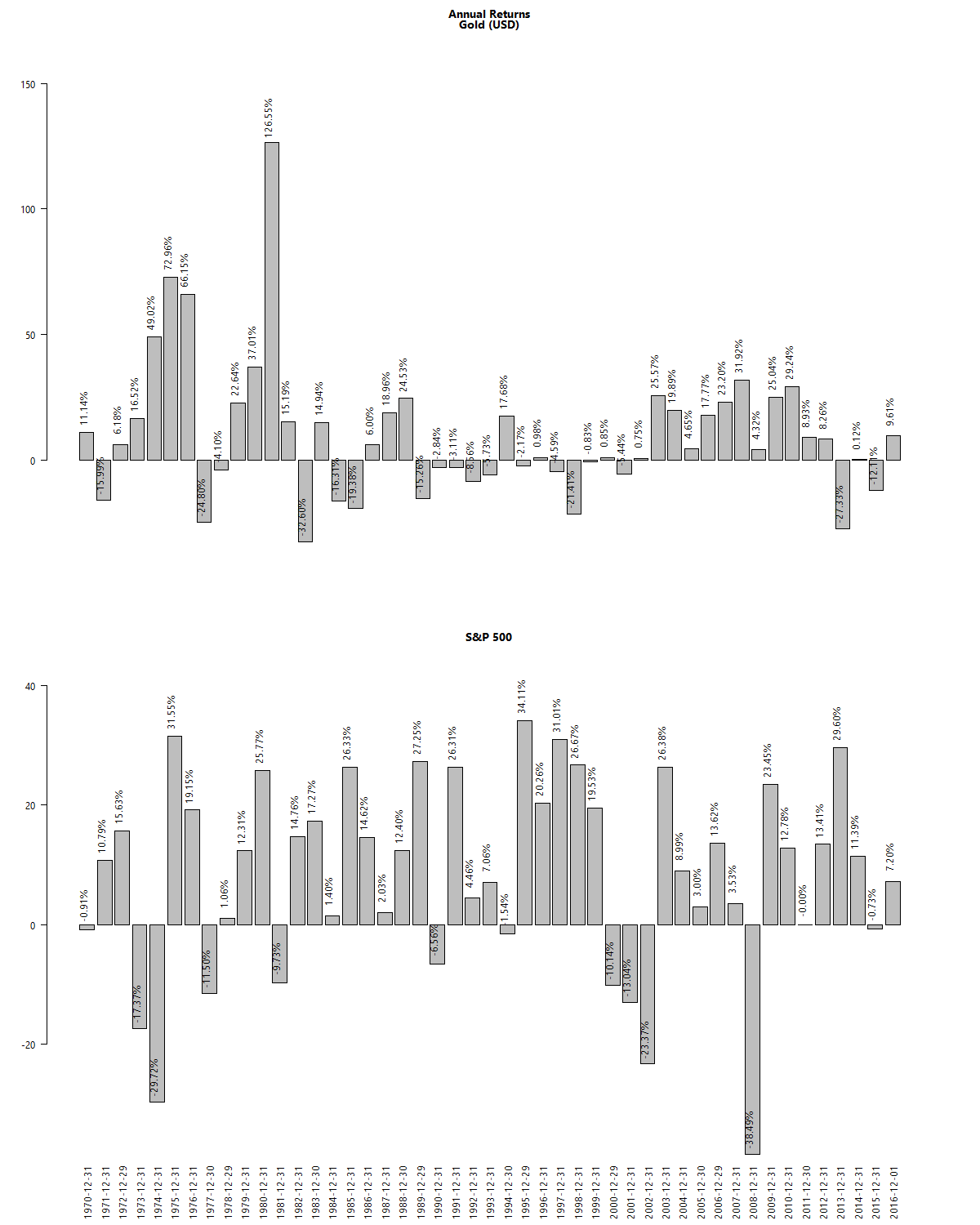
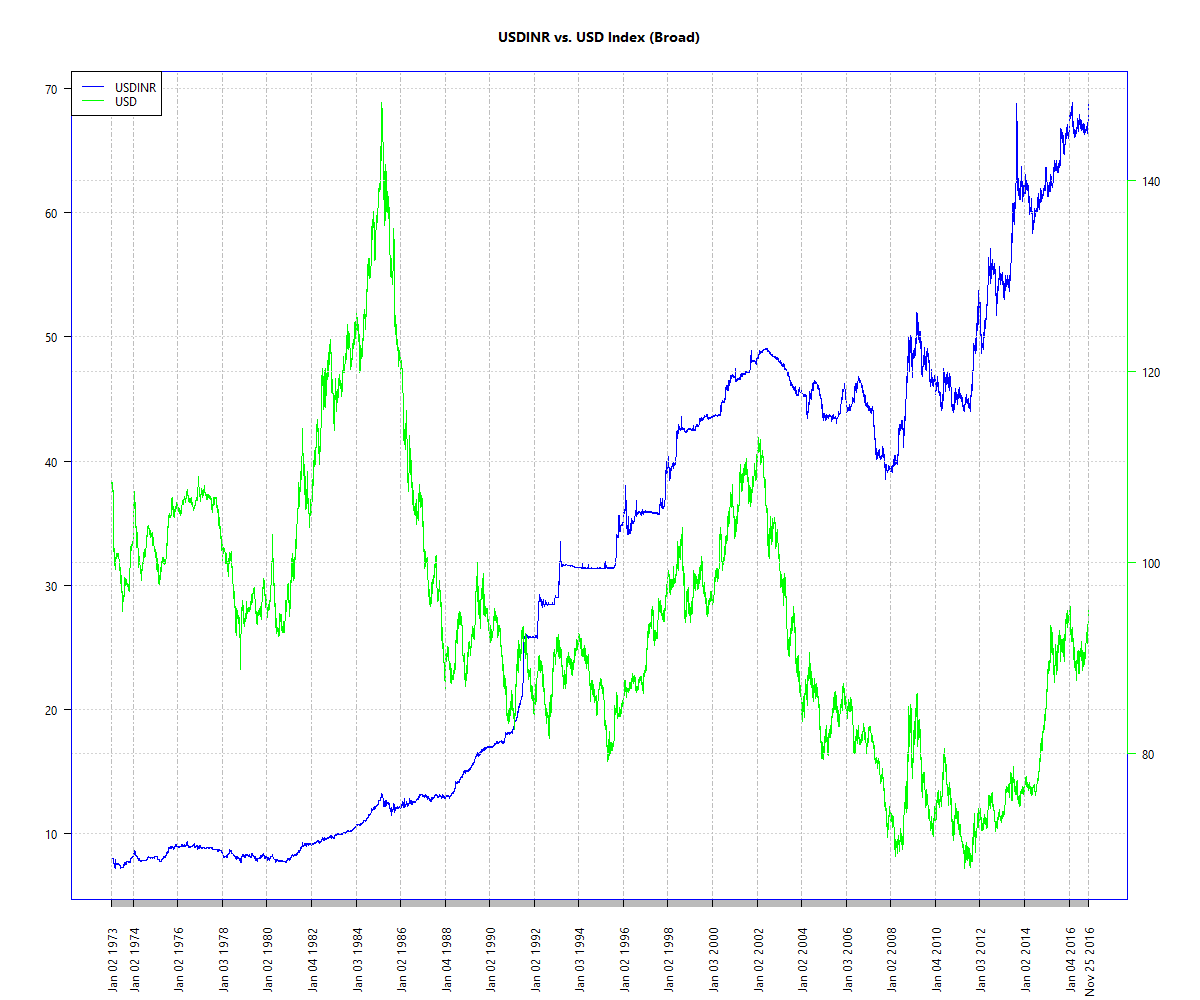
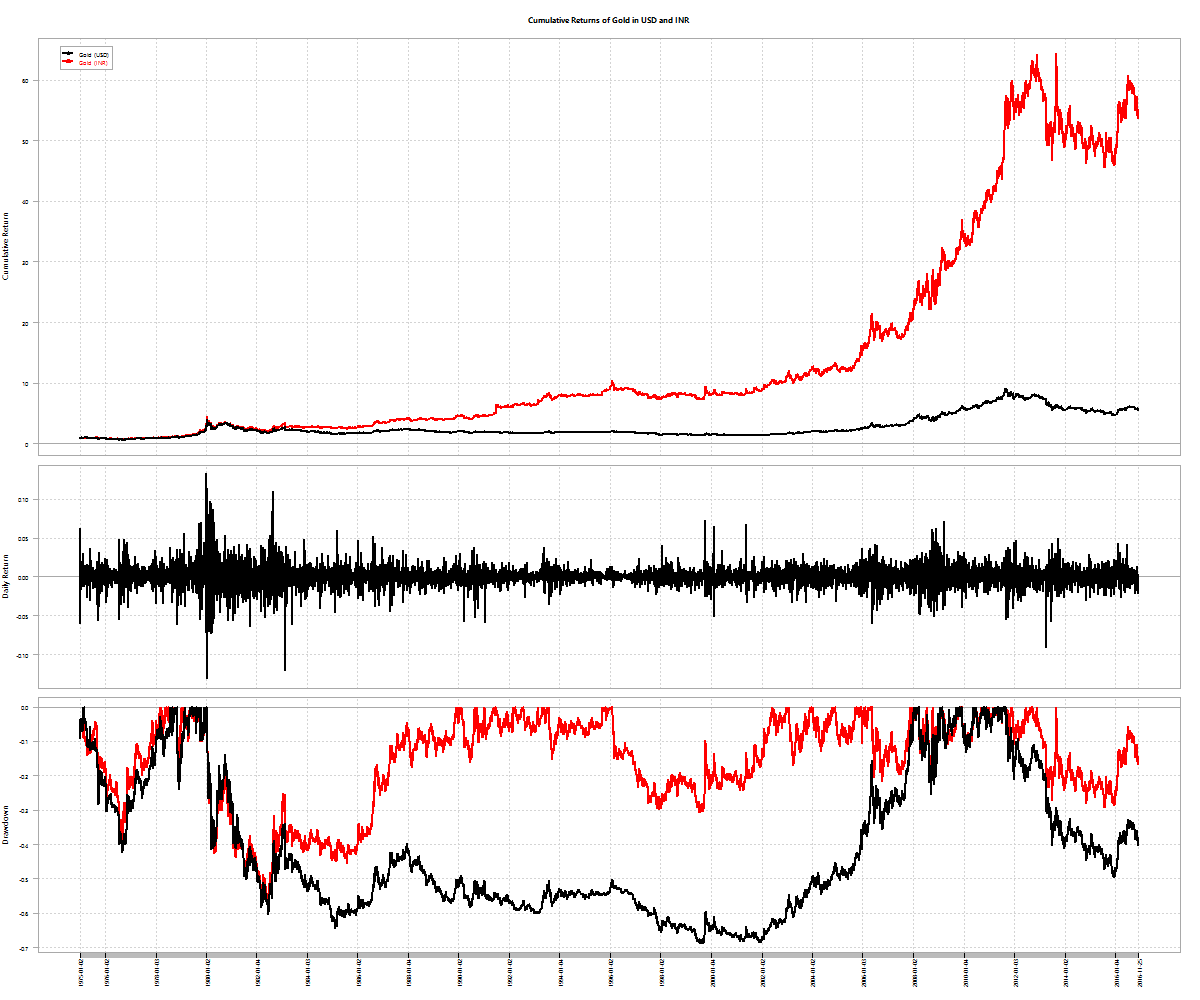
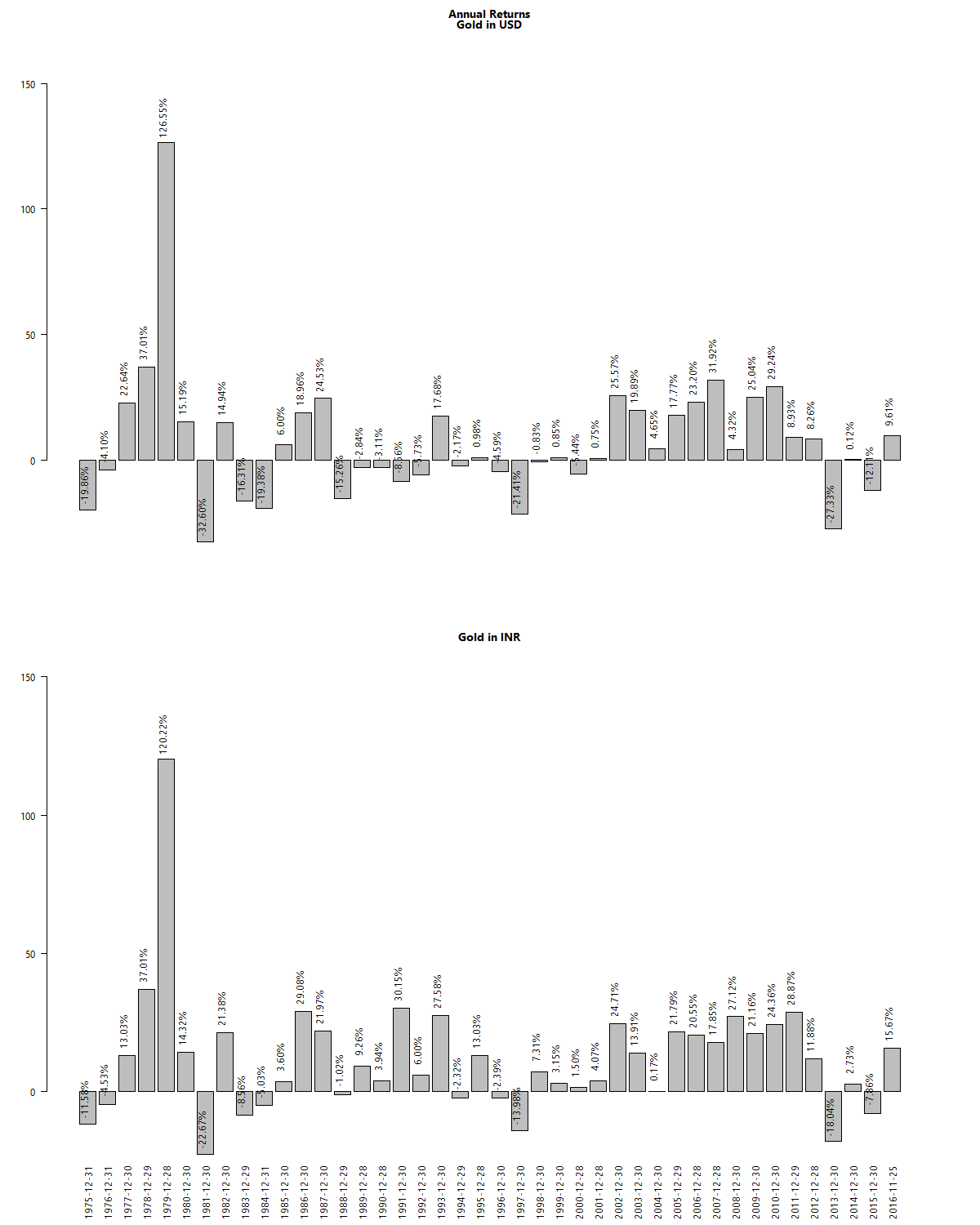
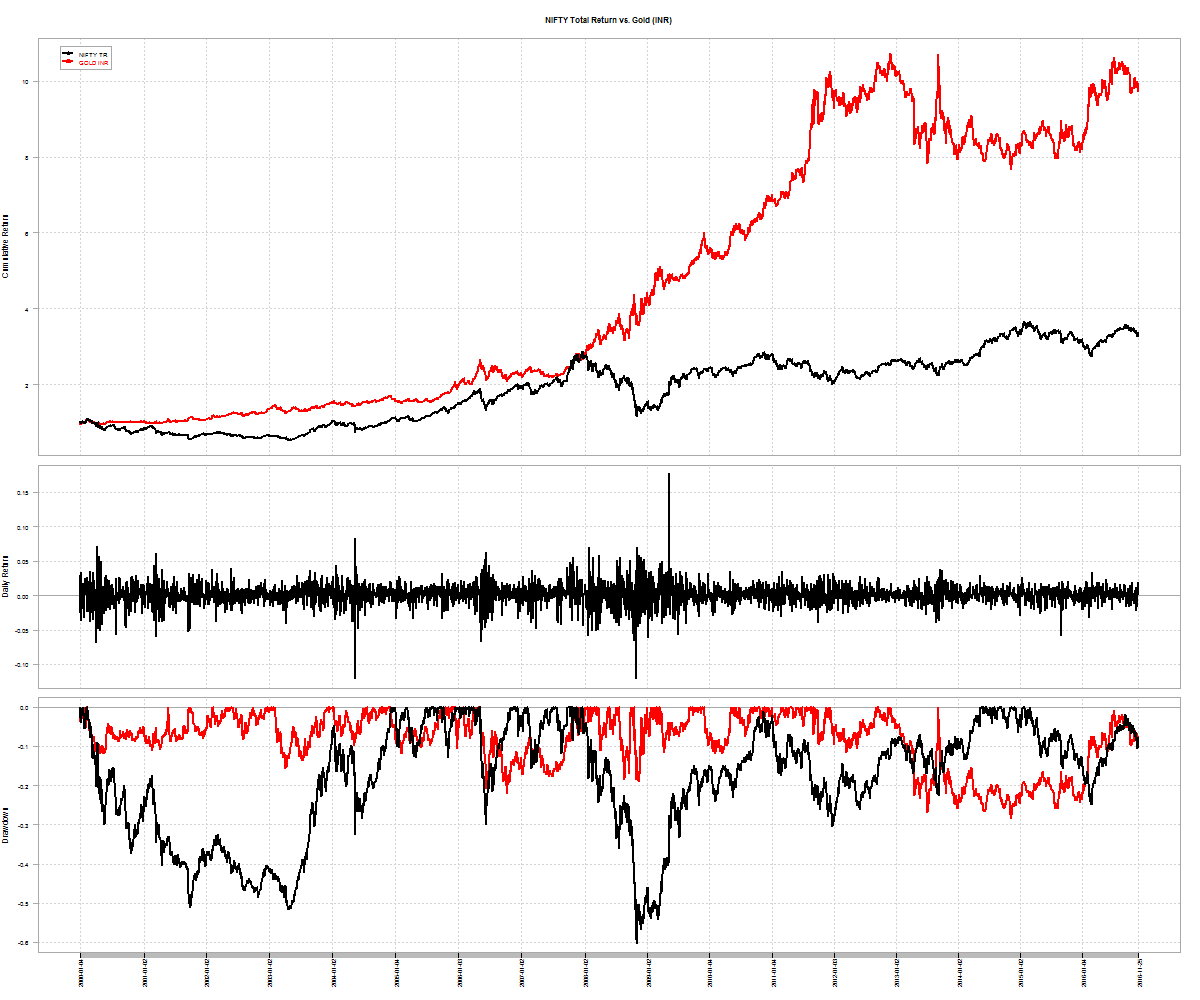
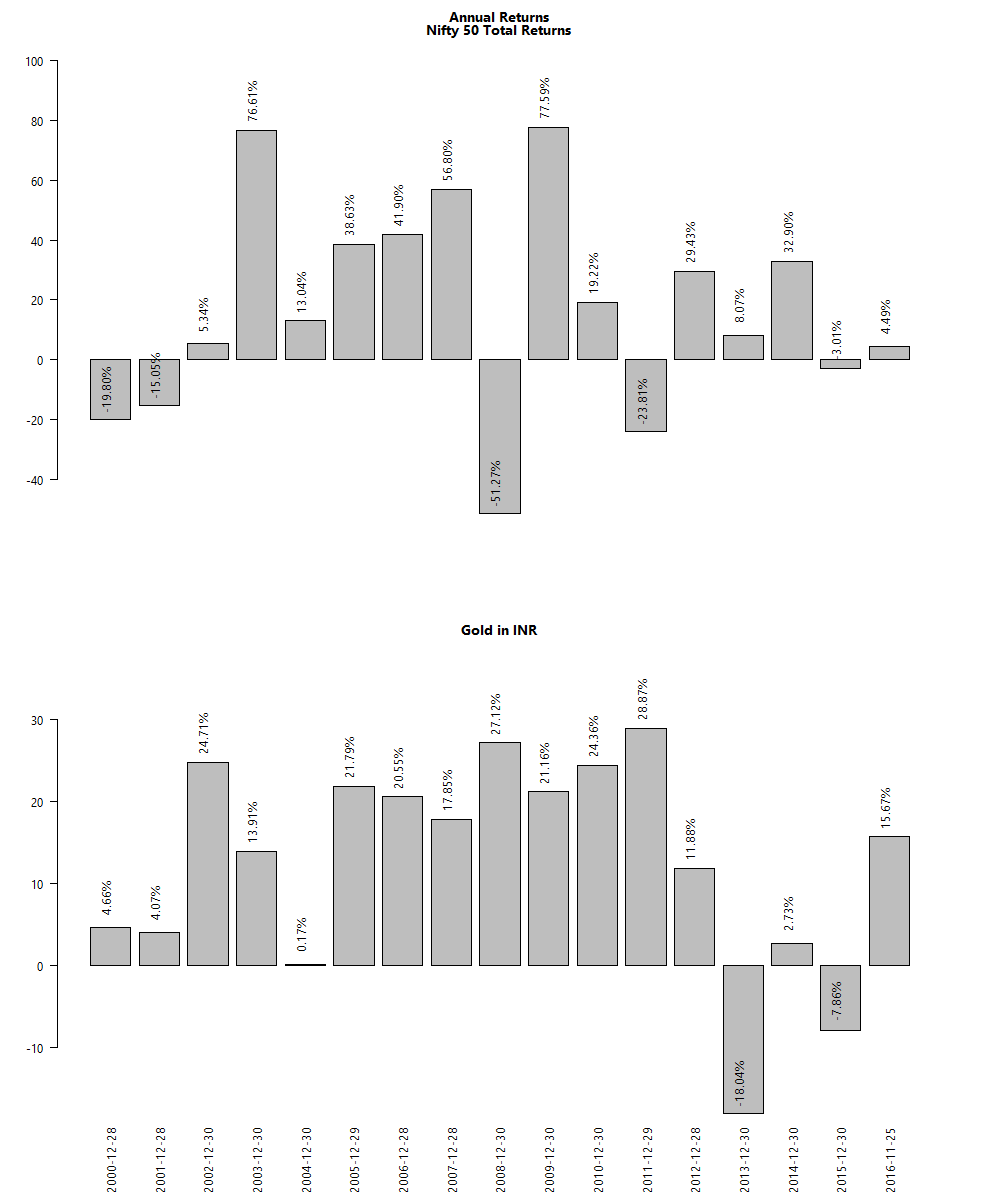
The assets we selected previously – MIDCAP, 0-5yr bond and NASDAQ-100 – were based on low observed historical pair-wise correlations. Most investors tend to add a fourth asset – gold – to their portfolios. Not only is gold not correlated with the other three, it has the added benefit of being priced internationally but traded locally. This allows it to benefit from rupee depreciation even if international gold prices remain flat. Observe how, at times, gold has a negative correlation to other assets:

The results
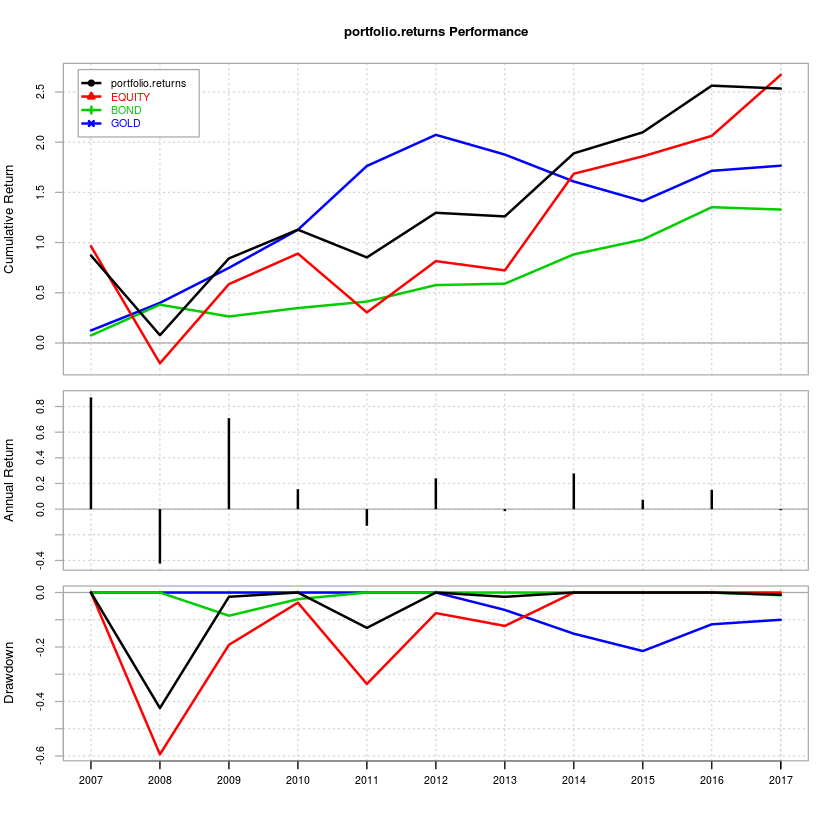
In the cumulative return and drawdown chart below, A1 is the MIDCAP index, A2 is the 0-5yr bond index, A3 is the QQQ and A4 is gold. A tax drag of 10% and an STT of 0.1% is applied at every rebalance. The rebalance threshold is set at 20%. The light-blue lines are the resulting portfolio returns. In the case of optimized portfolios, assets are allowed to have a weighting between 10% and 40% during the optimization process.
Equal Weighted

Variance optimized

Variance optimized
Expected Tail Loss optimized
Pre- and Post-tax returns
Rebalance
The rebalance threshold ends up determining the frequency of rebalance events. For a variance optimized portfolio, contrast the difference between a 20% threshold and an 80% threshold:
Take-away
- Every time there is a rebalance, the tax-man cometh and taketh away. Trying to minimize taxes is equivalent to minimizing the number of rebalancing events.
- To minimize reblancing events, one could set the threshold of rebalance higher. But there is a point of inflection with regards to after-tax returns.
- Allowing a single asset to balloon in weight risks larger portfolio drawdowns if that asset deflates.
- A four-asset equal weight portfolio under-performs a 3-asset equal weight portfolio. Gold maybe a good diversifier, but it doesn’t appear to do any favors to the portfolio on the performance front.
- Equal-weight 4-asset portfolio containing gold (above) drew-down less than the equal-weight 3-asset portfolio during the 2008 carnage (~30% vs. ~40%, respectively.)
Adding gold to a portfolio does not look like a good idea when looked through the lens of asset allocation schemes discussed here. However, there is a strong case for owning gold and the Sovereign Gold Bond (SGB) Scheme makes a lot of sense. See our previous post regarding the case for owning gold in India here.
Code, charts and the complete result dataset are available on github.