Correlation
When we discussed banks and introduced pair trading, we pointed out that a pairs trading strategy involves answering these questions:
- How do you identify “stocks that move together?”
- Should they be in the same industry?
- How far should they have to diverge before you enter the trade?
- When is a position unwound?
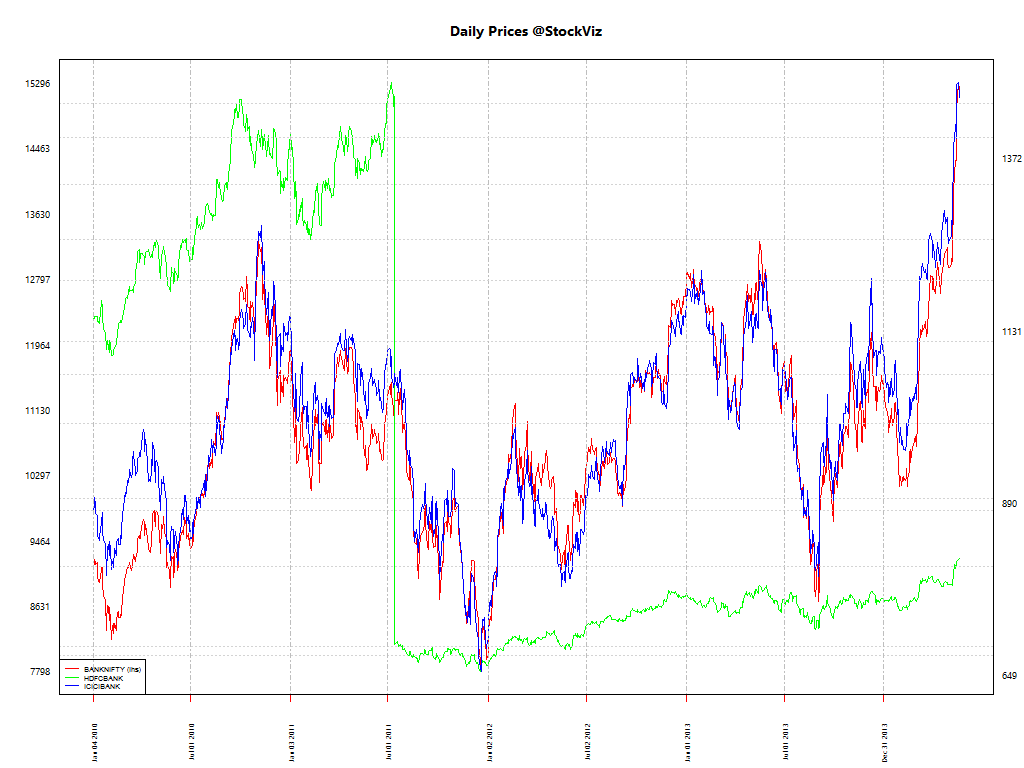
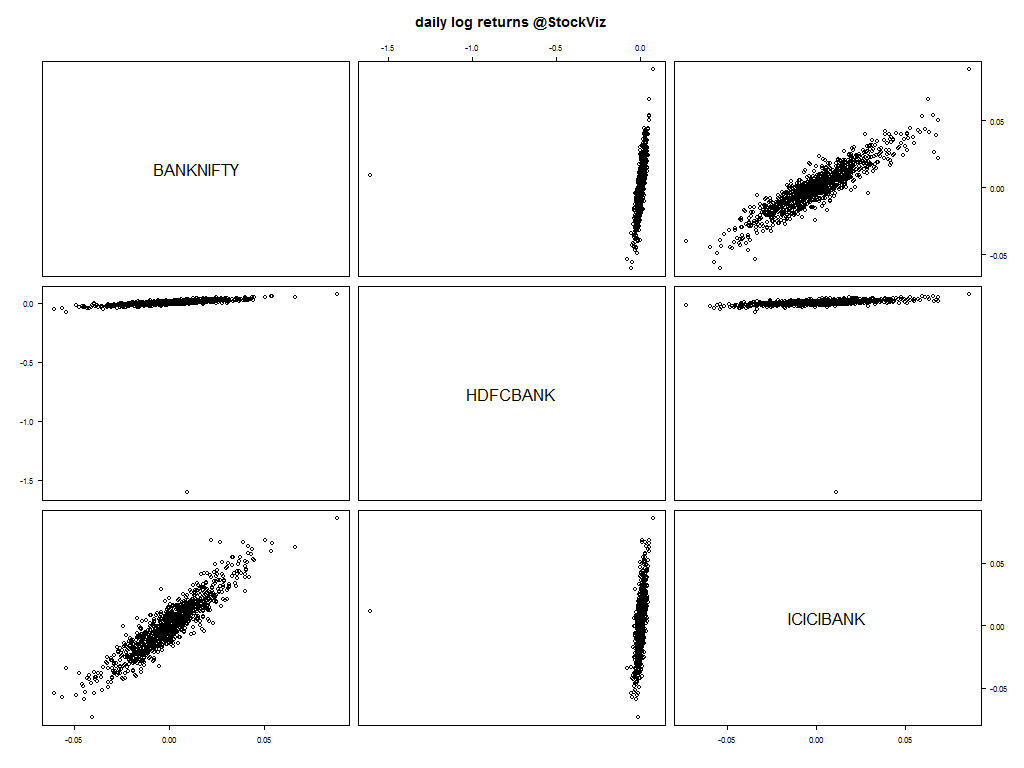
Traders new to pair trading often mistake the correlation of prices to be indicative of “similarity”. For example, consider the Bank Nifty, HDFC Bank and ICICI bank. Here’s the chart of the closing price of the nearest to expiration futures contract:
And there are some really tight correlations:
| BANKNIFTY | HDFCBANK | ICICIBANK | |
|---|---|---|---|
| BANKNIFTY | 1.0000000 | 0.7419966 | 0.9462238 |
| HDFCBANK | 0.7419966 | 1.0000000 | 0.8327847 |
| ICICIBANK | 0.9462238 | 0.8327847 | 1.0000000 |
However, this is only part of the story. What we need are pairs who’s price movements are mean reverting. Looking at price correlation alone is not enough.
Spreads
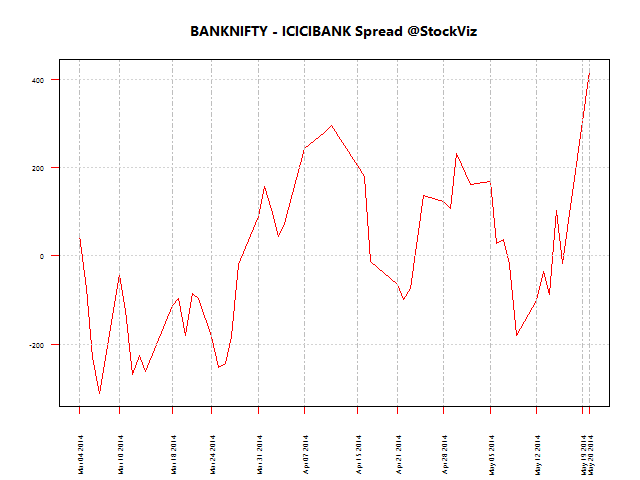
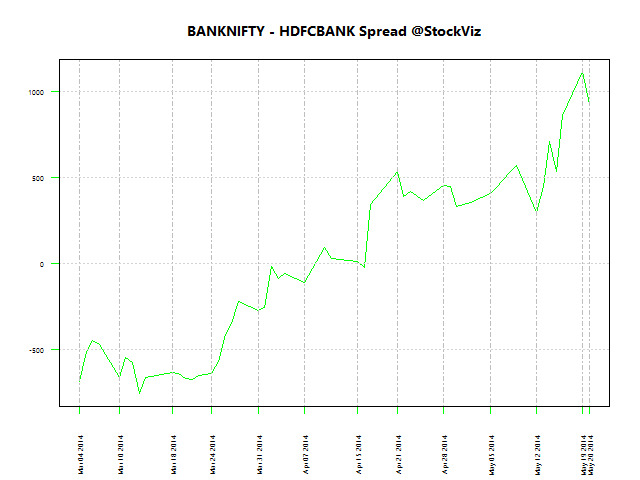
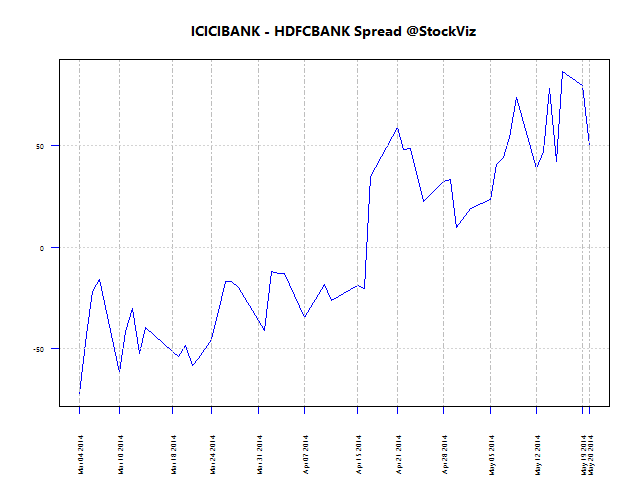
We need the spread between pairs to be “stable”, i.e., mean reverting.
spread = A – βB
where A and B are prices and β is the first regression coefficient.
200-day spreads
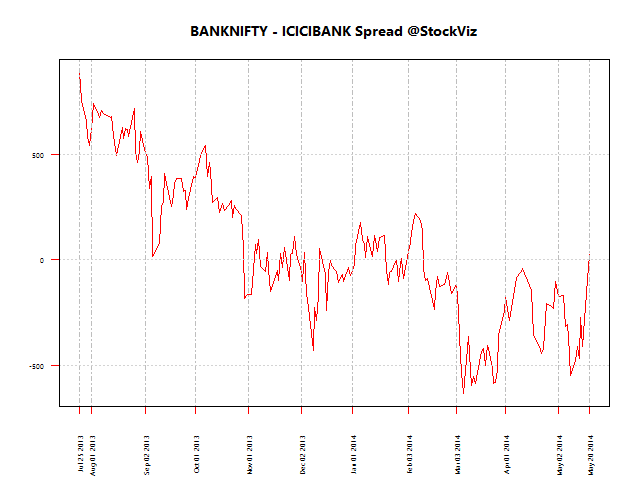
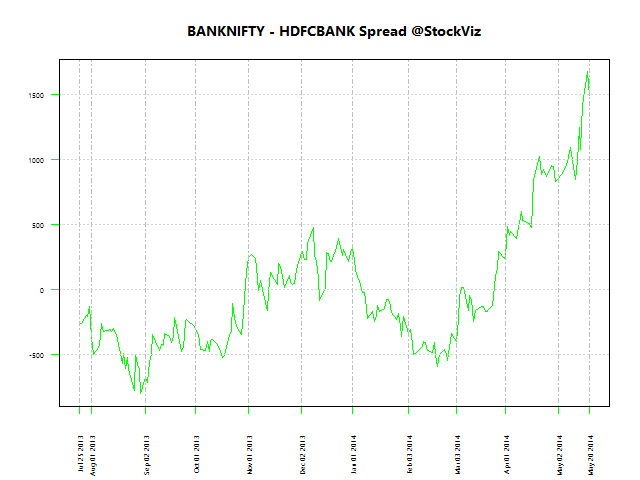
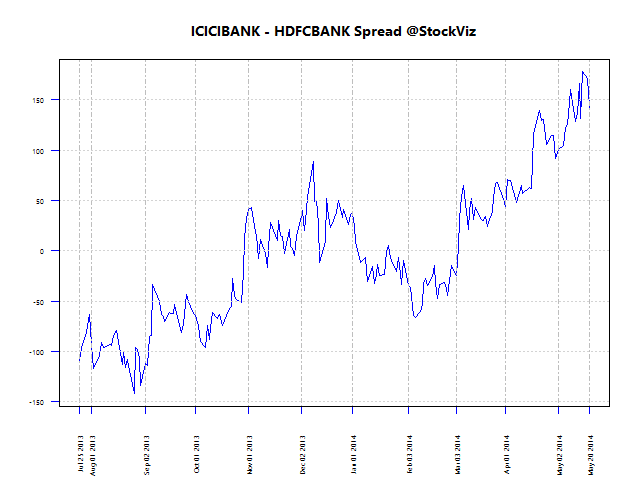
Here are the spreads between these pairs using 200-day data for regression:
50-day spreads
Here are the spreads between these pairs using 50-day data for regression:
Testing for cointegration
You don’t have to visually inspect spreads to see if they are mean-reverting. The most straightforward way of checking if a time-series is co-integrated is to perform a Dickey-Fuller test on it. If the p-value is less than 0.10, then this could be a good pair for trading.
| N | Pair | p-value |
|---|---|---|
| 300 | BANKNIFTY vs. ICICIBANK | 0.010000 |
| 300 | BANKNIFTY vs. HDFCBANK | 0.904480 |
| 300 | ICICIBANK vs. HDFCBANK | 0.407347 |
| 200 | BANKNIFTY vs. ICICIBANK | 0.010000 |
| 200 | BANKNIFTY vs. HDFCBANK | 0.472129 |
| 200 | ICICIBANK vs. HDFCBANK | 0.037115 |
| 100 | BANKNIFTY vs. ICICIBANK | 0.223806 |
| 100 | BANKNIFTY vs. HDFCBANK | 0.980776 |
| 100 | ICICIBANK vs. HDFCBANK | 0.670717 |
| 50 | BANKNIFTY vs. ICICIBANK | 0.429057 |
| 50 | BANKNIFTY vs. HDFCBANK | 0.405498 |
| 50 | ICICIBANK vs. HDFCBANK | 0.133357 |
| 30 | BANKNIFTY vs. ICICIBANK | 0.570427 |
| 30 | BANKNIFTY vs. HDFCBANK | 0.057717 |
| 30 | ICICIBANK vs. HDFCBANK | 0.370011 |
If you are trading futures, then a 200-day fit may not make much sense. The latest 30-day test between BANKNIFTY and HDFCBANK has a surprisingly low p-value of 0.057, indicating that there is a potential trade there.
To be continued…
Related articles
- Bank Nifty vs. HDFC Bank and ICICI Bank (stockviz.biz)