Tag: backtest

Global Equities Momentum, Part II

shyam January 25, 2019 0

In our previous post on Global Equities Momentum, we explored how we could potentially replace the indices used in the GEM decision tree with their momentum counterparts to boost returns. Corey Hoffstein (@choffstein) pointed out that given the excess turnover of momentum strategies, measuring their trend maybe adding too much noise. Also, could using value indices, given their lower turnover, make more sense?

We setup the following backtest to fix the first problem and explore the second.

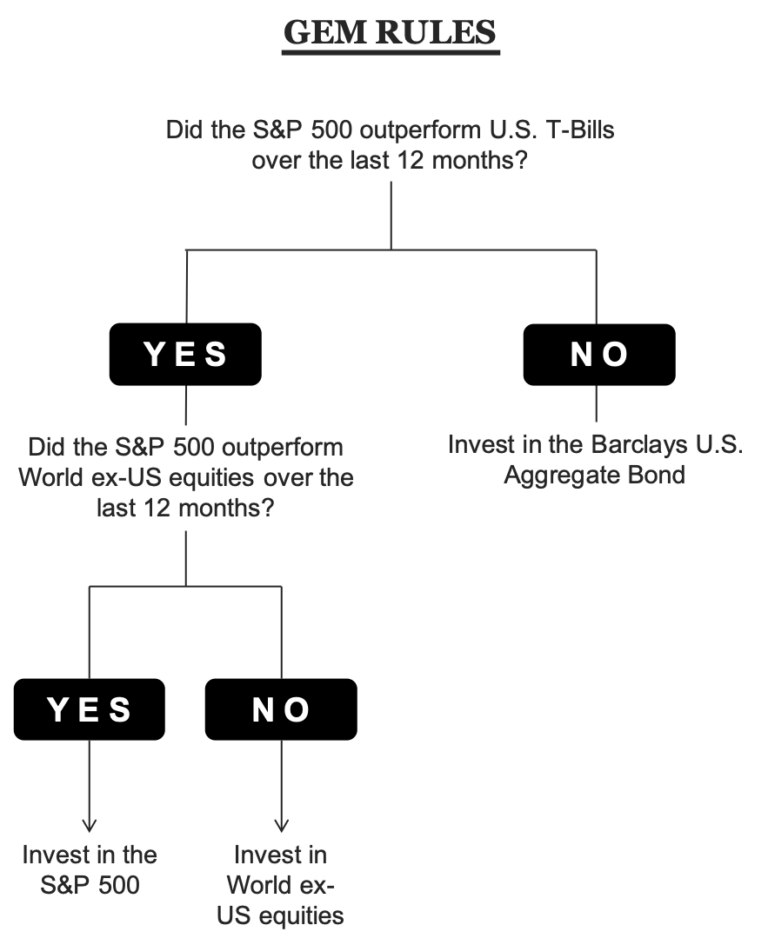
We will use the S&P 500 index to make the first decision of the GEM model: Should we invest in equities or bonds?
Once we get past #1, we will use different sets of indices to make the next one: USA or ex-USA? And trade the same.
We will use the MSCI USA PRIME Value index to represent US Value and MSCI ACWI ex USA PRIME Value index and MSCI WORLD ex USA PRIME Value index, in turn, to represent international value.

USA/All World ex-USA Value GEM

USA/Developed World ex-USA Value GEM

The GEM models both show vastly better returns and shallower drawdowns compared to buying and holding the underlying indices alone.
There is not a lot of difference between the two GEM models.
However, there are no equivalent ETFs for investors interested in implementing either of these GEM models.

In contrast, USA Momentum/MSCI World ex-USA Momentum:

Not only does the momentum GEM vastly outperform the value GEMs, it can be easily implemented with the MTUM and IMTM etfs.

Before jumping into any of these strategies, it is worth asking: Is this just data mining? How can we be sure that these backtests are statistically valid? By the same token, how can we be sure that even the dual-momentum model is robust? Gary Antonacci’s GEM backtest goes as far back as 1971 but we only have MSCI index data starting from 1995 or later. Besides, we are not sure if it is even possible to construct a reasonable momentum index going that far back. So, caveat emptor!

Code and more charts on github.

Categories Investing Insight Tags backtest, momentum

Global Equities Momentum

shyam January 22, 2019 0

Gary Antonacci created the Global Equities Momentum (GEM) model that applied dual momentum to stock and bond indices. It toggles between stocks and bonds using 12-month trailing returns. And when it toggles to “stocks,” it chooses between US equities and International (ex-US) equities based on whichever posted higher returns in the previous 12-months. Newfound Research has a chart that puts it across succinctly:

The model uses the S&P 500 index as a stand-in for US equities and the WORLD ex USA index for international stocks. However, there is nothing in the construction that prevents us from replacing those market-cap based indices with momentum based ones.

US Momentum / Market-cap International

Scenario 1: keep everything the same, except in the last stage, instead of buying S&P 500, buy US Momentum (SP 500×1).
Scenario 2: swap out S&P 500 and put US Momentum everywhere in the decision tree (MOM).

In the cumulative return chart below, the black line is the base case. It represents GEM as originally designed. The red line is Scenario 1 above, green is Scenario 2.

Even though Scenario 2 has higher returns, it comes at the cost of higher drawdowns. Scenario 1 seems to strike a compromise.
Base case drawdowns:

Scenario 1 drawdowns:

Scenario 2 drawdowns:

US Momentum / International Momentum

What if, we bought International Momentum (WORLD ex USA MOMENTUM) instead of the market-cap based WORLD ex USA?
Scenario 3 (dark blue): keep everything the same, except in the last stage, instead of buying S&P 500, buy US Momentum. And instead of buying market-cap international, buy WORLD ex USA MOMENTUM (SP 500×2).
Scenario 4 (light blue): swap out S&P 500 and put US Momentum everywhere. And instead of buying market-cap international, buy WORLD ex USA MOMENTUM (MOMx2).

Scenario 3 drawdowns:

Scenario 4 drawdowns:

Here are returns broken down annually for all the scenarios discussed above:

It appears that using the S&P 500 index for making decisions about buying US vs. World ex-US momentum boosts returns while keeping a floor under drawdowns.

Code and charts are on github.

Categories Investing Insight Tags backtest, momentum

Streaks, Part II – Backtest

shyam January 3, 2019 0

In Part I of this series, we saw that it is very rare for two consecutive down months to be followed by a third one. Here, we present a simple backtest that goes long NIFTY 50 for a month if the previous two months were negative.

The shallow drawdowns of this strategy makes it ideal for leveraged trades. NIFTY futures are about 7x levered. That should transform the 190% gross return to about 1330%, beating buy and hold by a wide margin. The MIDCAP 100 index behaves similar to this between the 2005 through 2018 time-frame. However, the results are not so great if you include data prior to 2005.

This looks like a case of severe data-mining and should be discounted as such. But it is an interesting result nevertheless.

Code and charts are on github.

Categories Investing Insight Tags backtest, quant

SMA Distance, Part III – Backtest

shyam December 26, 2018 0

In Part II, we saw that when the 50- and 100-day SMA Distance is in the first quintile, subsequent 20-day returns have smaller left tails. Can that observation be turned into a market-timing system?

The backtest

We setup two long-only portfolios: one that goes long S&P 500 if either of the 50-day or 100-day SMA Distance is in the first quintile and another that, in addition to the 50- and 100-day being in the first quintile, also makes sure that the 200-day SMA Distance is not in the first quintile. These are L1 and L2 in the chart below:

Using SMA Distance is a poor long-term strategy. However, it does help avoid deep drawdowns. It is not very useful as a standalone indicator but perhaps could be used to confirm other signals.

Code and charts are on github.

Categories Investing Insight Tags backtest, sma

VIX and Equity Index Returns, Part II

shyam November 13, 2018 0

Please read Part I for the introduction.

Holding-period back-test

In Part I, we ran a quick back-test that would go long the equity index if the VIX was in a certain quintile and saw how the 5th quintile produced the lowest draw-down returns. The index was held only for a day. However, our box-plot of VIX quintile vs. subsequent n-day returns begs us to look at alternate holding periods as well. What would the returns be if we held onto the index beyond a day?

Here is how long-only S&P 500 returns when VIX is in the 5th quintile, across different holding periods looks like:

The problem with this strategy is that when there is a steep fall in the index, the VIX keeps going higher and will be in the 5th quintile for an extended period of time. Have a look at the 2008-2009 segment in this chart:

What happens if we used the change in VIX to time the equity index?

VIX returns deciles

If we bucket VIX returns (percentage change over previous close over n-days, 1000 trailing observations) into deciles and observe the next 5, 10, 15 and 20-day returns of the underlying index over them:

There is no determinable pattern here. Perhaps the VIX and the index are co-incident with none holding the power of prediction over the other.

Interested readers can browse the github repo for corresponding Nikkei 225 and NIFTY 50 charts.

Categories Investing Insight Tags backtest, VIX, volatility