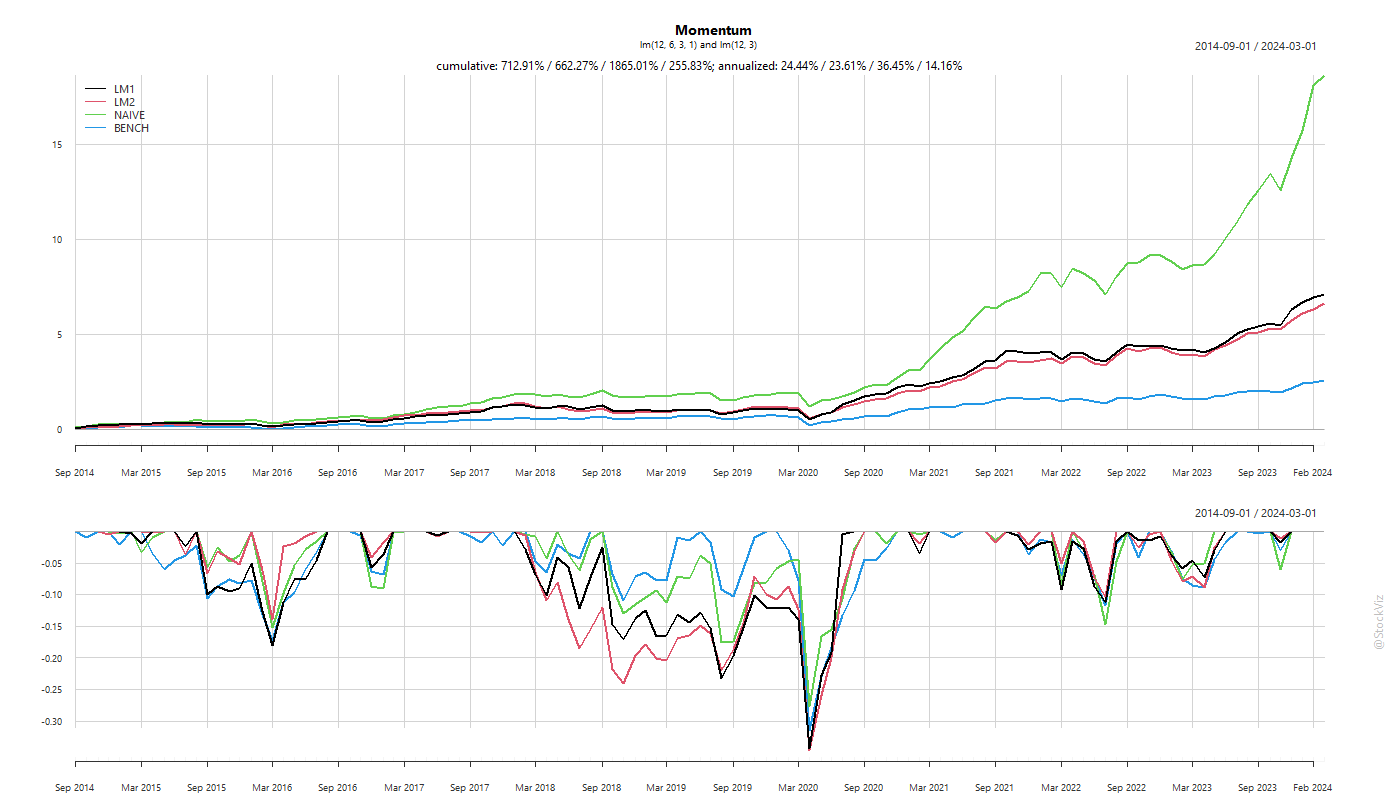
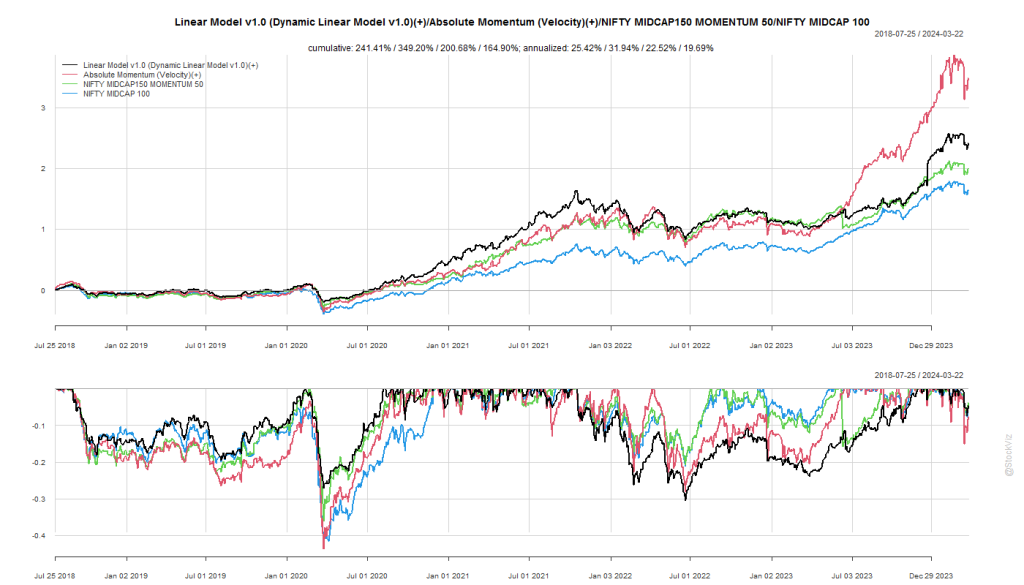
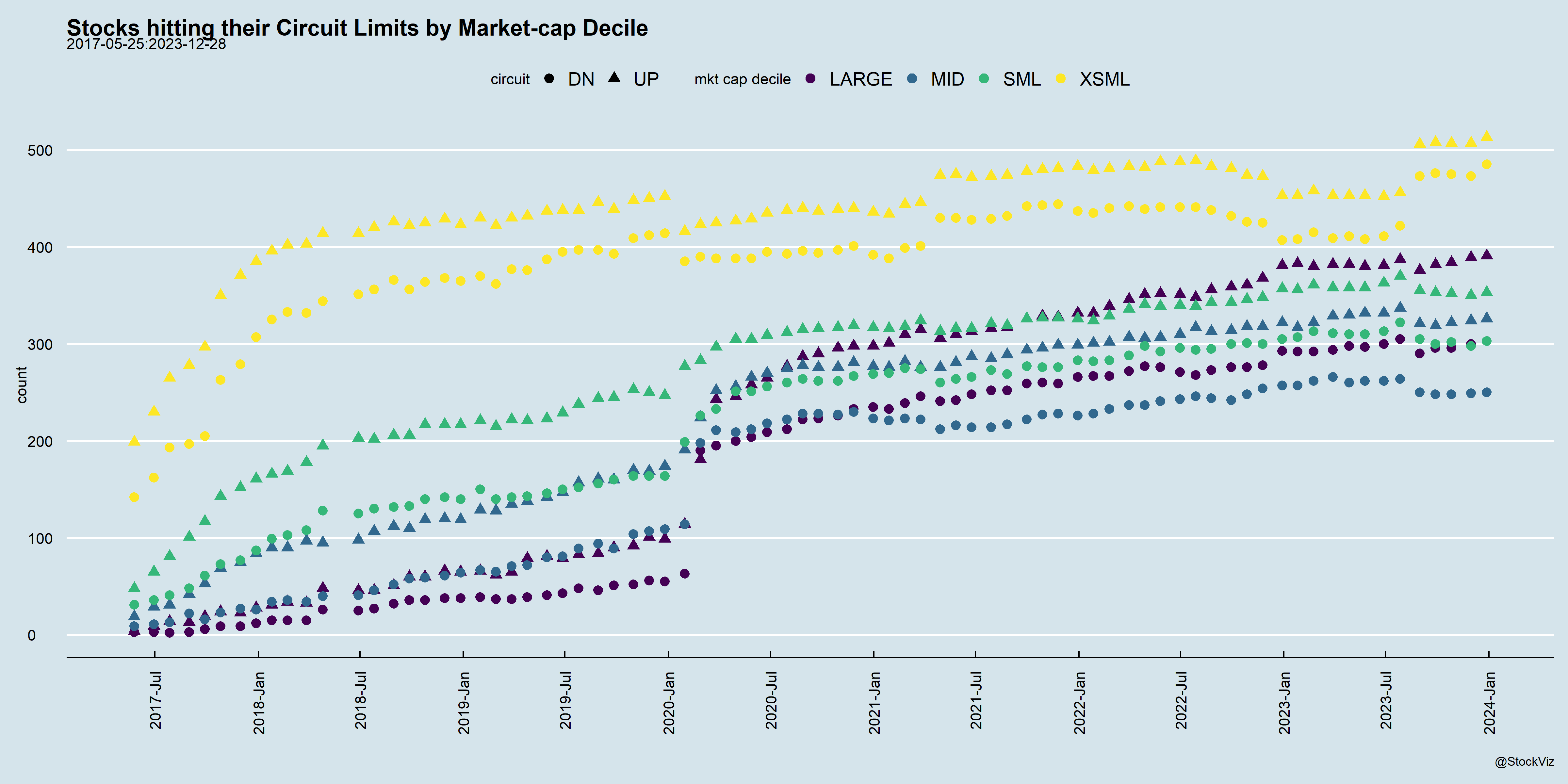
Previously, we discussed how overnight volatility is not necessarily the scary boogeyman that it is made out to be. However, what maybe true for the NIFTY may not be true for other indices. For example, commodity stocks could carry larger overnight risks than, say, FMCG stocks.


If you look at the median volatilities of the two indices, commodity stocks have larger close-close volatility than FMCG stocks. However, FMCG stocks have lower volatility in general, so not sure if the differences are meaningful.
What about QQQs (US tech) and XLE (US Energy)?


Most energy related reports are released during US market hours while earnings reports are not. That could explain why XLE relative overnight volatility is lower than QQQ’s? Also, weekend risks averaging less than daily and overnight risks is surprising as well.
Code and charts on github.