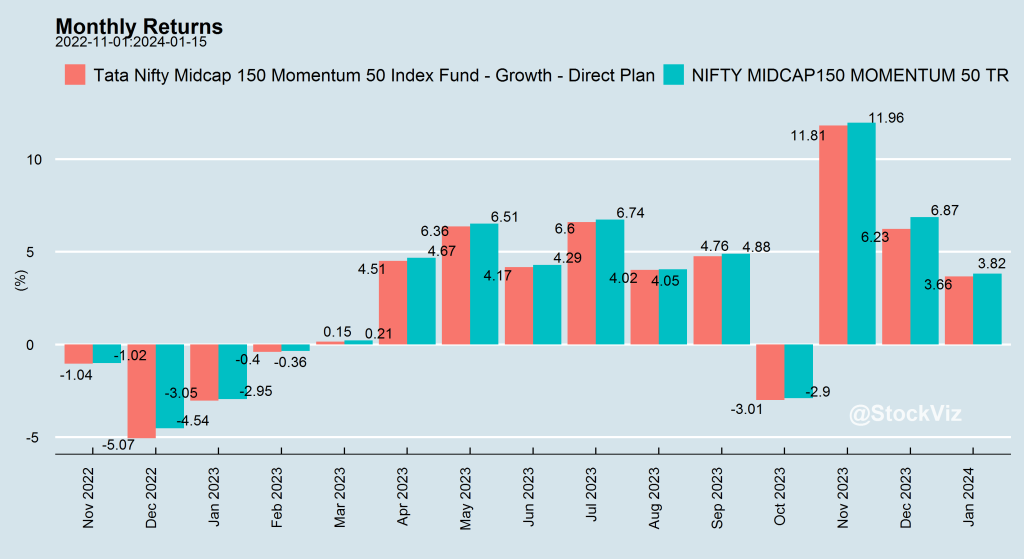
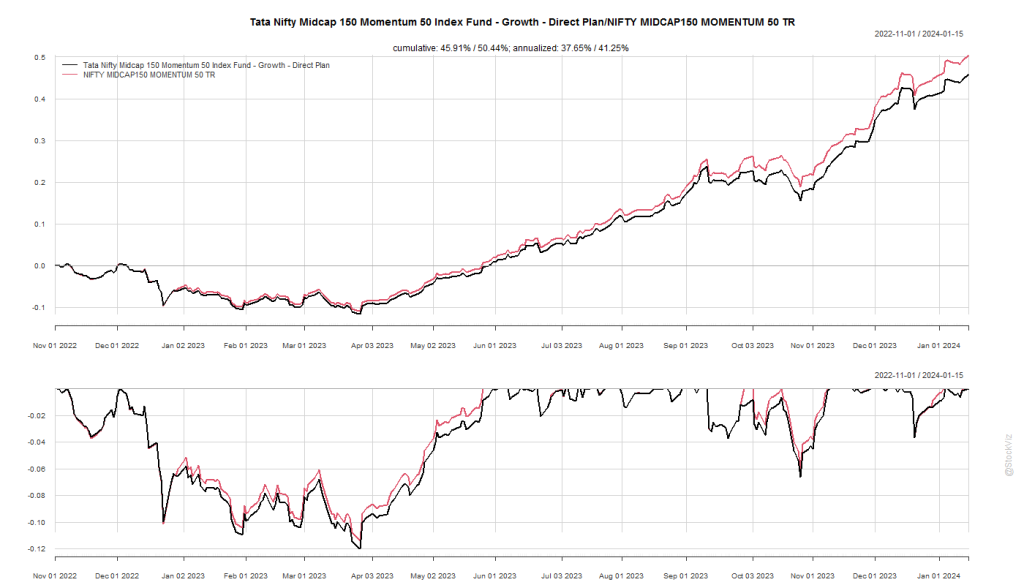
Our previous post discussed how liquidity drops exponentially as the market cap gets smaller. This illiquidity also means that a lot of micro-cap stocks spend their time out of the market.
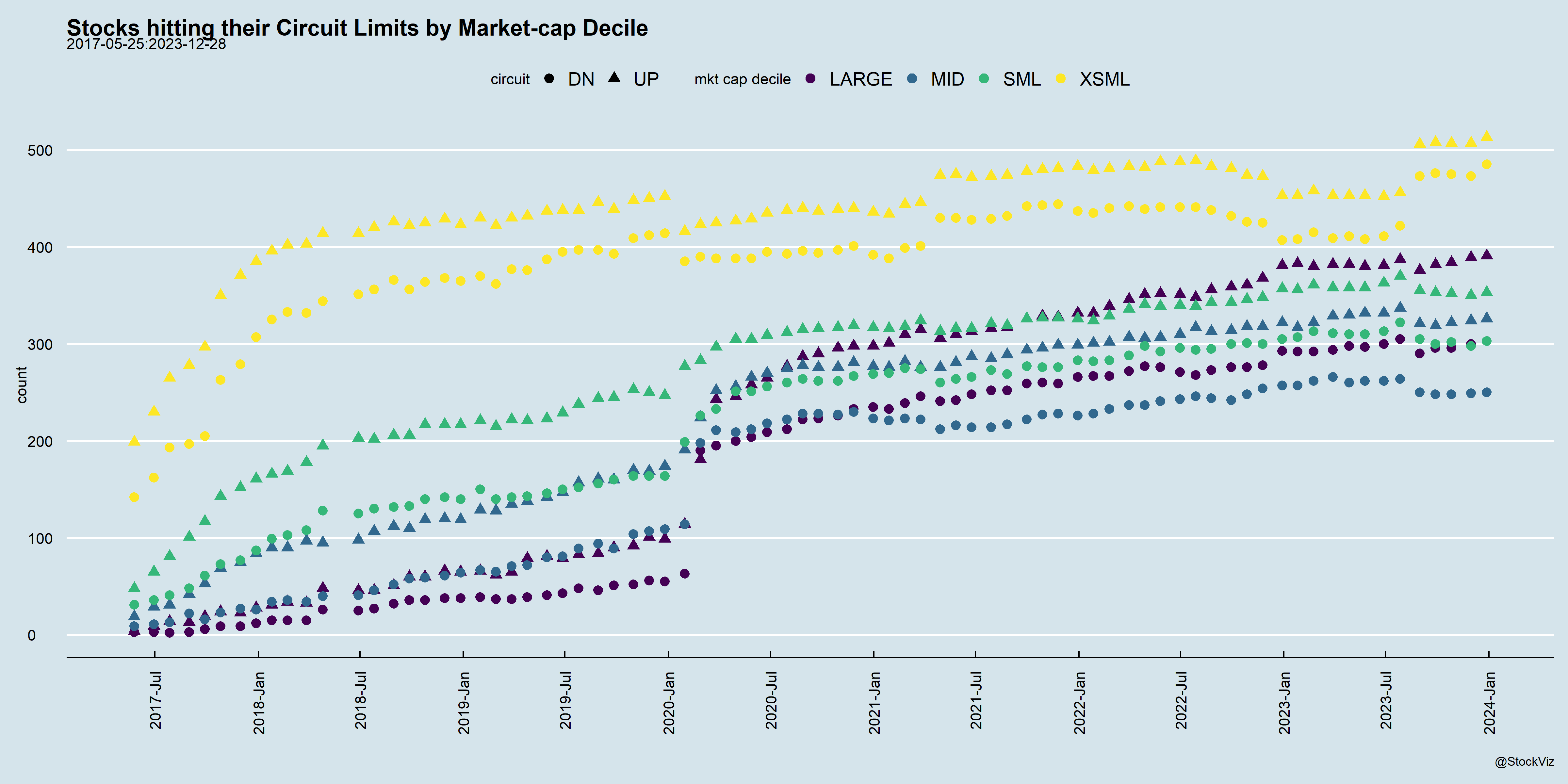
This is a problem for direct equity investors in micro-caps if they actually try to bank the price appreciation they might have seen in the stocks that they own. And a bigger problem for momentum algorithms in the small-cap space.
Index funds in the micro-cap space have yet to go through a test of the liquidity mismatch between allowing redemptions at daily NAV vs. not being able to trade the underlying stocks for days on end.
Bull markets allow us the luxury of coming up with a plan for something that has plenty of historical precedent.