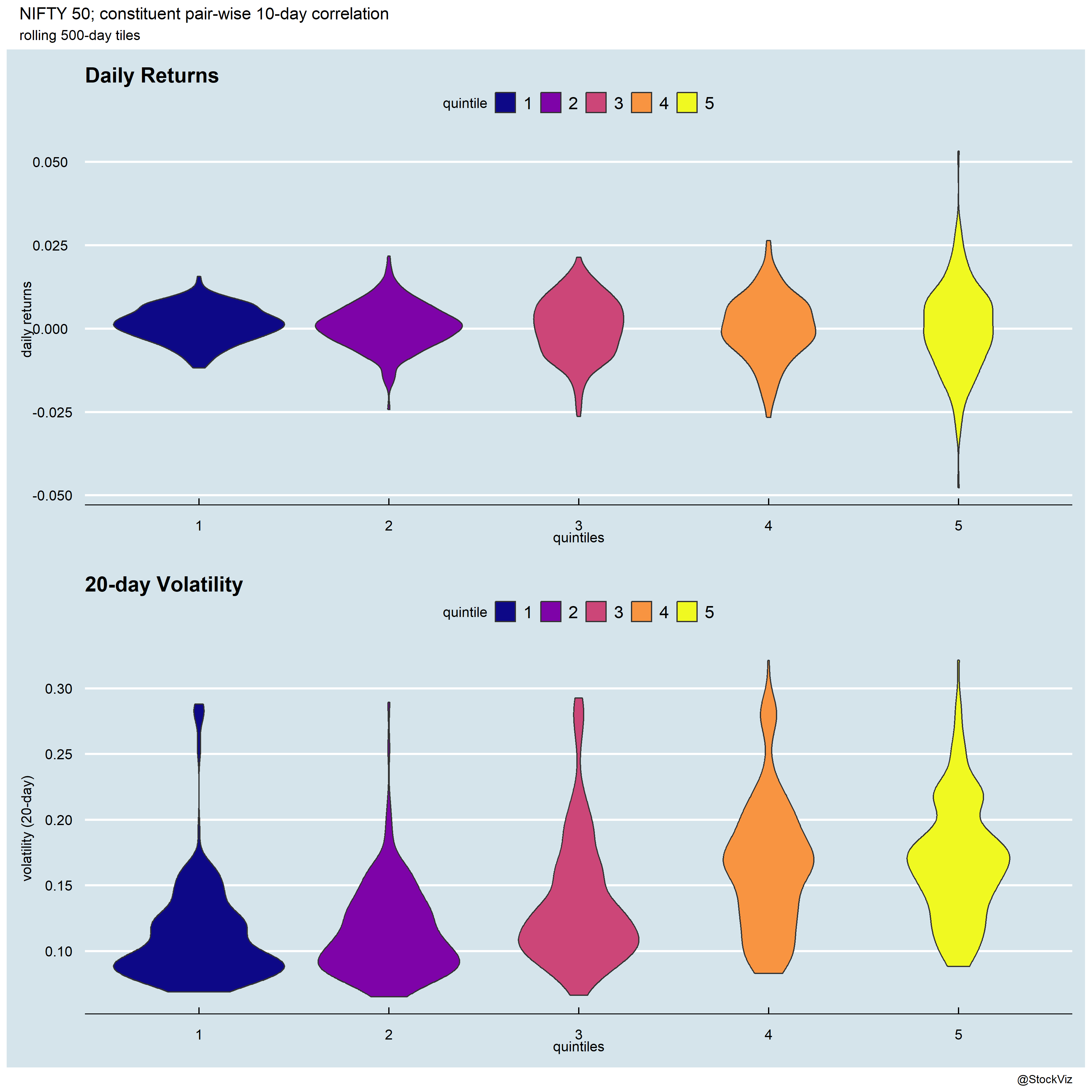
Realized Semi-variance is a measure of intraday volatility. It is nothing more than the sum of squared high-frequency positive and negative returns.

It is typically used for forecasting volatility. However, can it be used for market timing? After all, volatility is said to be sticky and avoiding downside volatility is supposed to be desirable.
What if, you exit the market when the current volatility is more than the historical average (based on some lookback)?

Turns out, doing something like that would’ve worked on the pre-pandemic NIFTY 50. Maybe not higher returns but better Sharpe than buy & hold.

However, post-pandemic returns have been disappointing.

The same thing can be observed on the MIDCAP 50 index as well.

We’ll add this to the growing pile of disappointing results of using volatility for directional bets.