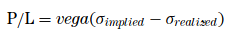More often than not, real time feeds are exposed as web socket streams. Web sockets are extremely sensitive to network glitches. Glitches – when the connection drops for a very small span of time – will cause your market data to lag badly as your client tries to reconnect/re-establish the feed, eventually leading to catastrophic failure.
The problem with glitches is that it is hard to work around. A complete drop in the connection can be handled by a router that can switch over to a backup connection. Glitches are more sinister.
For example, we have broadband connections from three different service providers (Hathway, Excitel and BSNL) to make sure our systems can stay connected. They all have varying degrees of stability and customer service. Here are the number of glitches per hour over the last few days:

You can work around 1-2 glitches an hour by making your re-connection logic more robust. However, there is no getting around the Hathway level of glitches.
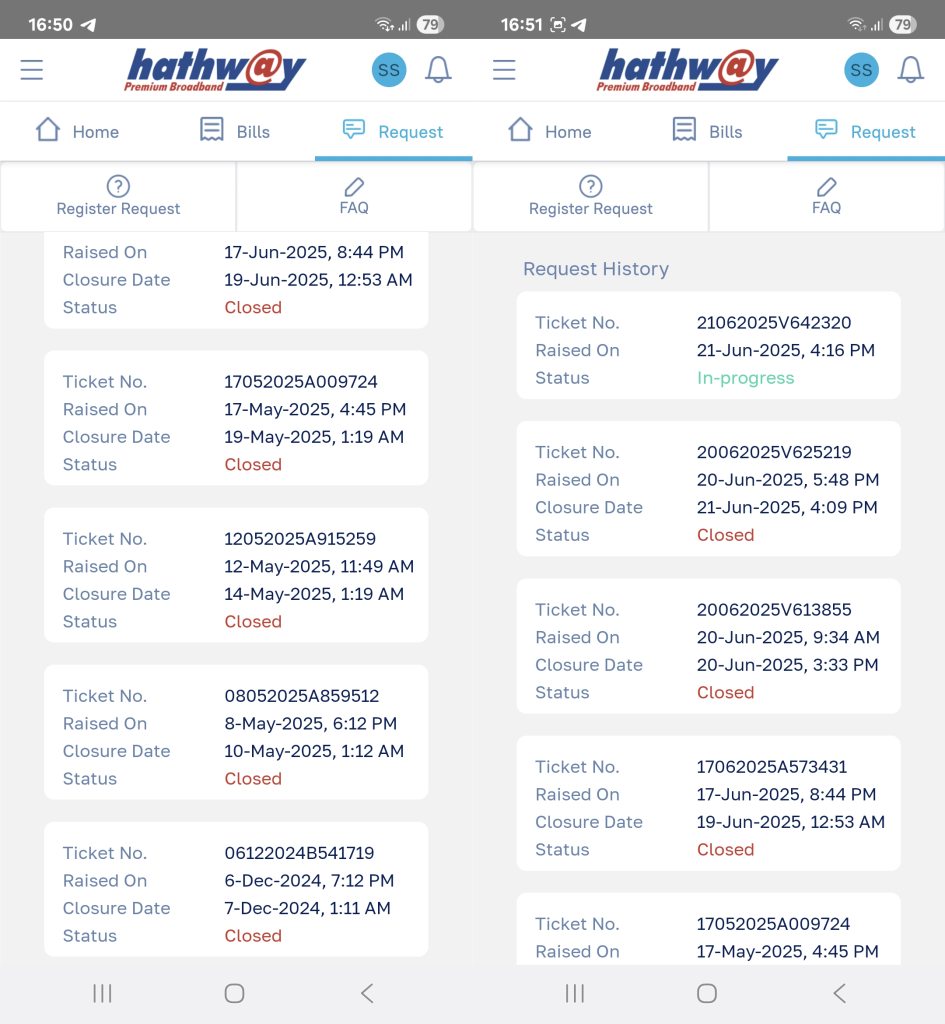
If your service provider itself is not monitoring for glitches, then explaining the problem to them is impossible. Support tickets get closed because “network is connected.” Here is a history of our support tickets with Hathway – an ongoing saga with no end:
As you scale, monitoring your infrastructure becomes increasingly important. Be aware that your service provider could be (willfully) blind to the specific issues you are facing – their job might depend on them not solving it. And, always have a backup and a backup for your backup.
The python code to monitor for glitches and the R code to draw the charts are on github.